 |
|
 |
|
3 - Cas des céviennes
[1 - Aspect historique] [2 - Preuve du théorème] [4 - Cas des points symétriques] [5 - Cas des points doubles]
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]
 |
|
 |
|
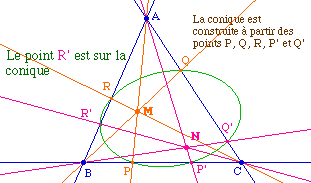 |
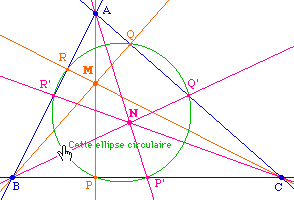
Théorème : Les droites joignant les sommets d'un triangle à deux points donnés coupent les côtés opposés en six points qui sont sur une même conique. En effet, par Céva on aEt donc par le théorème de Carnot, les 6 points sont sur une conique. |
![]() CarCev1a.fig (Preuves
proposées en exercice)
CarCev1a.fig (Preuves
proposées en exercice)
 |
|
 |
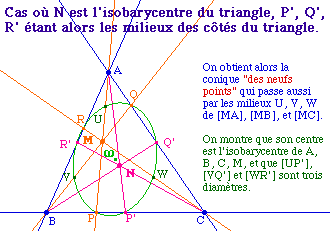
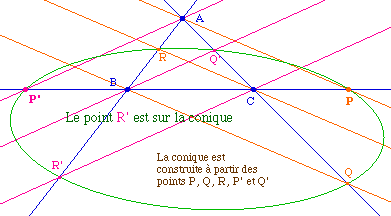
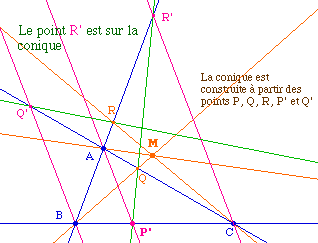 Cas particulier impropre |
[1 - Aspect historique] [2 - Preuve du théorème] [4 - Cas des points symétriques] [5 - Cas des points doubles]
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]