 |
|
5 - Cas des points doubles
[1 - Aspect historique] [I2 - Preuve du théorème] [3 - Cas des céviennes] [4 - Cas des points symétriques]
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]
 |
|
 |
|
 |
 |
Si, dans la relation du théorème de Carnot, on identifie les points P et P', Q et Q', et R et R', la conique est tritangente au triangle. Par ailleurs la relation devient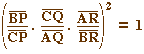 Si on exclu le cas où les trois points sont alignés (produit égal à 1 par Ménélaüs), alors le produit des trois termes est égal à -1, et, par le théorème de Céva, les droites (AP), (BQ) et (CP) sont parallèles ou concourantes. |
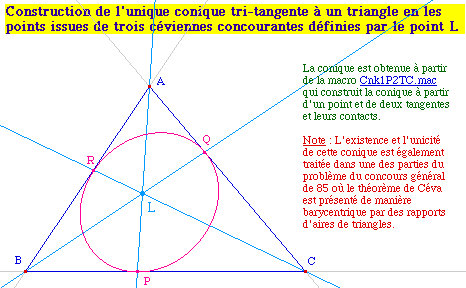
![]() CarDoub3.fig
(réalisée par la macro
CarDoub3.fig
(réalisée par la macro ![]() Cnk1P2TC.mac
de la page Applications de
"Pascal"
Cnk1P2TC.mac
de la page Applications de
"Pascal"
Sa transformée ![]() Cnk3TCC.mac
[CC pour Céviennes
Concourantes] : objets initiaux A, B, C, L.
Cnk3TCC.mac
[CC pour Céviennes
Concourantes] : objets initiaux A, B, C, L.
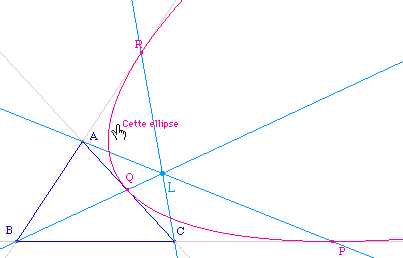
Une ellipse, et, en déplaçant le point L d'un pixel ...
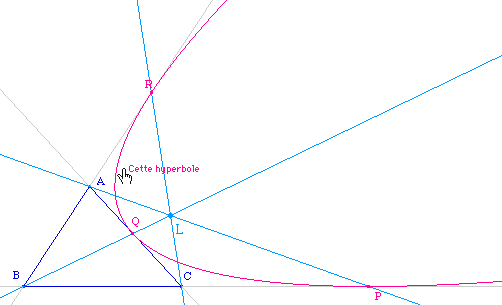
Une hyperbole, et entre les deux pixels ...
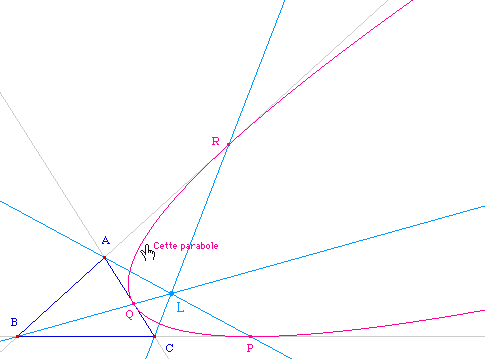
... bien-sûr, mais illustré
depuis une autre figure Cabri ![]() CarPar01.fig
comme on s'en doute ...
CarPar01.fig
comme on s'en doute ...
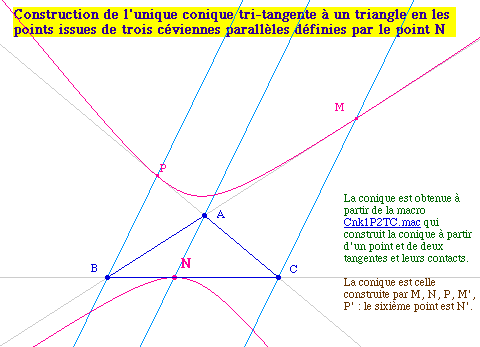
![]() CarDoub4.fig ou la macro
Cnk3TCP.mac
[CP pour Céviennes
Parallèles] : objets initiaux A, B, C et N de
(BC)
CarDoub4.fig ou la macro
Cnk3TCP.mac
[CP pour Céviennes
Parallèles] : objets initiaux A, B, C et N de
(BC)
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]