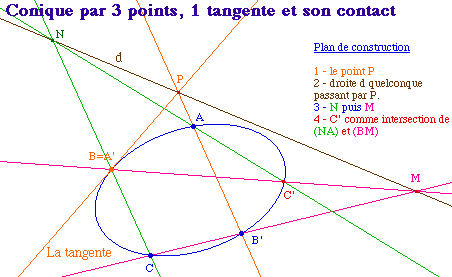
I.3 - Quelques Cabri-applications du théorème de Pascal
[I.1 - Introduction et exemples] [I.2 - Théorème de Pascal]
[I.4 - Théorème de Carnot par les coordonnées barycentriques]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]

Note technique : comme les trois points C, B', A ne sont pas alignés, l'une des deux droites (CB') ou (AB') n'est pas parallèle à la tangente. On peut donc appliquer la macro même si l'une des deux est parallèle à la tangente : il suffit de choisir pour deuxième et troisième point, ceux pour lesquels la droite n'est pas parallèle à la tangente.


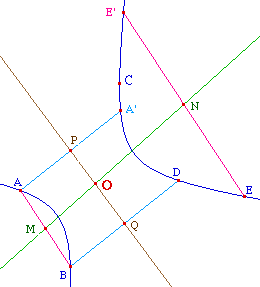 |
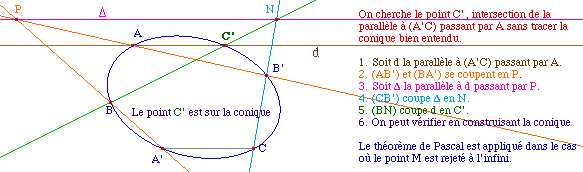
À partir de 5 points A, B, C, D et E, on peut, par la macro précédente, construire E' de la conique passant par ces 5 points, tel que (EE') // (AB) et A' tel que (AA') // (BD).On construit alors les droites des milieux des cordes parallèles (MN) et (PQ). Le centre de la conique est l'intersection de ces deux droites.Approche affine pour l'ellipse : le milieu des cordes parallèles est la version affine de la médiatrice d'une corde d'un cercle. Par transformation affine cette lecture affine donne le centre.Cas général (ellipse et hyperbole) : la droite (MN) est la polaire par rapport à la conique du point à l'infini dans la direction (AB), de même (PQ) est la polaire du point à l'infini dans la direction (BD). (voir aussi pôle et polaire)
|
[I.4 - Théorème de Carnot par les coordonnées barycentriques]
[Retour "Considérations affines et projectives"] [Retour Coniques]