[4 - Liens sur ce sujet] [Retour Algébre] [Menu général]


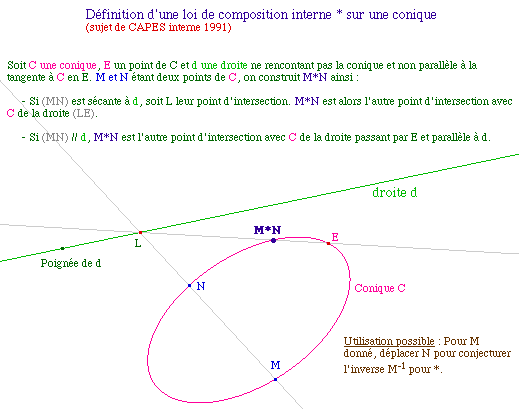
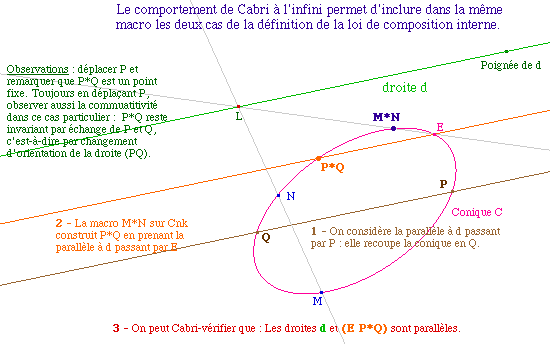
Par définition même, la loi * est commutative, et E est élément neutre.Dans le sujet de CAPES interne 91, la loi n'est définie que sur une ellipse, mais elle s'applique naturellement à toute conique : il suffit de savoir qu'une droite coupant la conique la coupe en deux points. Dans ce cas, on se place dans le plan projectif. Il faut alors ajouter pour l'hyperbole deux points (ses intersections avec la droite de l'infini) et dans le cas de la parabole, un point (son point de contact avec la droite à l'infini). Dans la figure précédente, il suffit de faire apparaître les points constituants pour vérifier l'application de la macro dans le passage à l'infini sur une hyperbole.

Le cas de la parabole
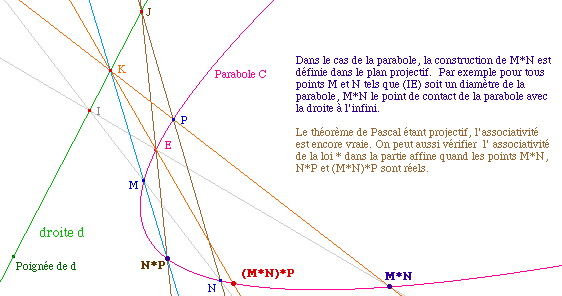
Position du problème
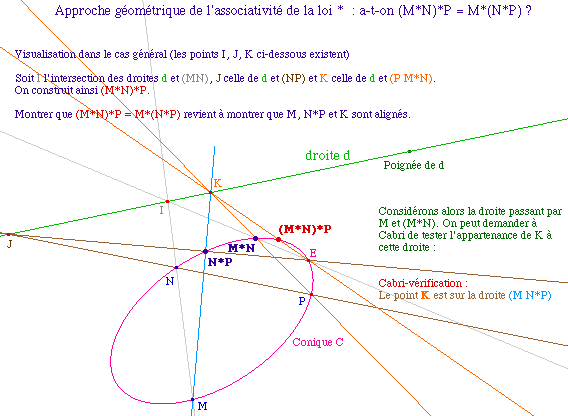
Preuve du résultat
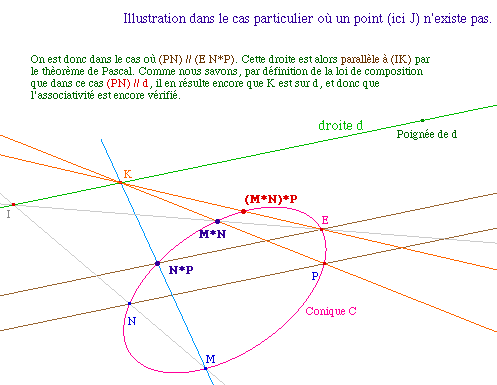
Redéfinissons le point K comme étant l'intersection des droites (M N*P) et (P M*N). Sur la conique C, nous disposons de 6 points E, M, N, P, N*P et M*N tels que les droites (E M*N) et (MN) se coupent en I, (E N*P) et (NP) se coupent en J et les droites (P M*N) et (M N*P) en K. On sait alors, d'après le théorème de Pascal sur l'hexagramme mystique, que les point I, J, et K sont alignés. Comme I et J sont sur d, le point K aussi.
L'associativité en résulte, en effet, la droite (KE) recoupe la conique en un point qui est à la fois (M*N)*P car K est que la droite (P M*N)) mais aussi M*(N*P) car K est aussi sur la droite (M N*P). Et donc (M*N)*P = M*(N*P).
Les cas particuliers
Le sujet du devoir s'intéressait essentiellement à ce cas général, le théorème de Pascal ayant été montré, dans une autre partie, d'abord sur un cercle, puis par affinité sur les ellipses dans les cas particuliers d'existence des points I, J et K. Nous savons qu'il s'applique aussi dans tous les cas particuliers, ce qui permet d'assurer que l'associativité est bien vérifiée dans ces cas particuliers. En voici quelques exemples :
GrpCnk05.fig
Le théorème de Pascal permet de prendre en compte tous les cas, comme par exemple :
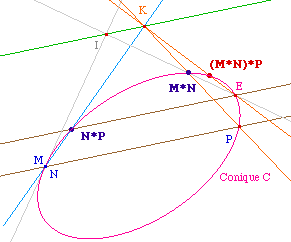
Ici M = N, (MN) est alors la tangente en M à la conique
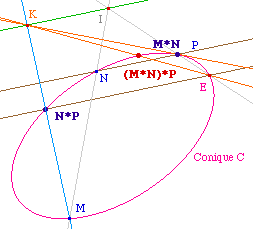
Cas où P est l'un des points précédents, ici P = M*N.

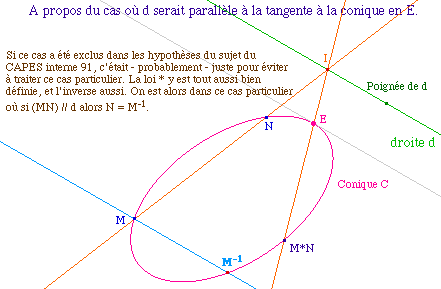
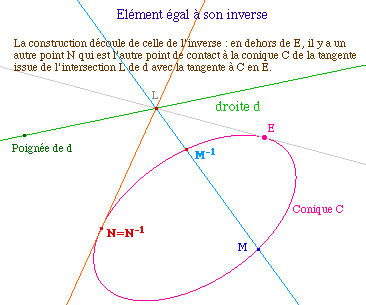
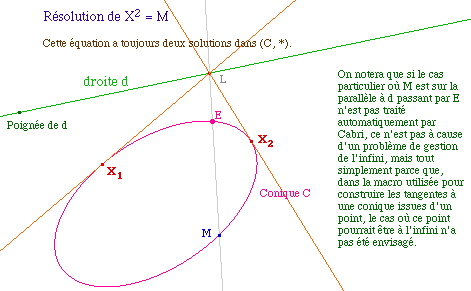
Remarque sur cette structure de groupe : si on sait qu'il existe une structure de groupe naturelle sur une cubique, il est naturel de "faire une cubique particulière" en adjoignant une droite à une conique : on construit en fait une structure sur une cubique en s'assurant que la conique soit un sous-ensemble stable pour la loi.
Pour un point de vue différent voir la page "Autres groupes"