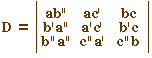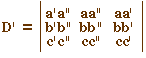Coniques en
coordonnées barycentriques
Ì.2 -
Théorème de Pascal - Premières
consèquences
[I.1 - Introduction et
exemples] [I.3 -
Applications du théorème de Pascal]
[I.4 - Théorème de
Carnot par les coordonnées barycentriques]
[Retour "Considérations
affines et projectives"] [Retour
Coniques] [Menu
Général]
Le
théorème de Pascal : illustrations et notations
utilisées (Claude Tisseron - Ed. Hermann)
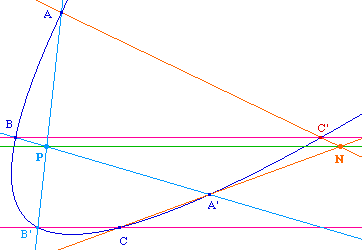
Six points A, B, C, A', B', C', dont trois ne sont
jamais alignés, sont sur une même conique si et
seulement si les intersections
P de (AB') et
(BA'),
N, de (AC') et
(CA') et
M de (BC') et
(CB') sont
trois "points alignés".
Illustrations - Preuve - Consèquences
Illustration dans le cas
général
 Pascal01.fig
Pascal01.fig
|

|
Pour illustrer le théorème de Pascal dans
le cas particulier de la parabole, on peut utiliser la macro
 Para4pts.mac
déjà proposée à cette
page, qui, étant donnés 4 points,
construit les deux paraboles passant par ces 4 points (ici
on n'en a conservé qu'une).
Para4pts.mac
déjà proposée à cette
page, qui, étant donnés 4 points,
construit les deux paraboles passant par ces 4 points (ici
on n'en a conservé qu'une).
 Pascal02.fig
Pascal02.fig
|
Illustration dans le cas où l'une
des trois intersections n'existe pas (par exemple M)
Dans ce cas les coordonnées barycentriques de
l'intersection deviennent les coordonnées du vecteur directeur
des deux droites parallèles (BC') et (CB'). Le
théorème s'étant à ce cas en
interprétant l'expression "points
alignés" par le fait que le vecteur dirige la droite
(NP).
 Pascal03.fig
Pascal03.fig
 Pascal04.fig (Cas de la parabole)
Pascal04.fig (Cas de la parabole)
Illustration dans le cas où deux des
trois intersections n'existent pas
Le théorème s'étend encore à ce cas
en interprétant l'expression "points
alignés" par le fait que la troisième
intersection n'existe pas, et donc que ces trois vecteurs vecteurs
dirigent les directions des côtés deux à deux
parallèles. Autrement dit, un cas très particulier du
théorème de Pascal veut qu'un hexagone formé de
côtés opposés deux à deux
parallèles est toujours inscrit dans une conique.
 Pascal05.fig
Pascal05.fig
Voir une illustration
esthétique de ce cas particulier dans le
théorème de Morley, ou encore une
structure de groupe sur les coniques utilisant ce même cas
particulier.
Illustrations - Preuve -
Conséquences
Preuve du
théorème de Pascal par les coordonnées
barycentriques (Tisseron)
Théorème :
Six points A, B, C, A', B', C', dont trois ne sont jamais
alignés, sont sur une même conique si et seulement si
les intersections
P de (AB') et
(BA'),
N, de (AC') et
(CA') et
M de (BC') et
(CB') sont
trois "points alignés".
On se place dans le repère affine (A, B, C), ainsi
l'équation barycentrique d'une conique passant par ces trois
points est uyz +
vzx + wxy =
0, avec u, v, w non tous nuls.
Notons alors les coordonnées barycentriques de A', B', C'
par A'(a, a', a"), B'(b, b', b") et C'(c, c',c").
Calcul des coordonnées
barycentriques de M, N et P - Condition d'alignement
À partir de A (1, 0, 0) et B'(b, b', b"), des
coordonnées tangentielles de (AB') sont A ^ B' soit (0, -b",
b'). De même, on trouve pour coordonnées tangentielles
de (BA') : B ^A' soit (a", 0, -a). Et donc, les coordonnées de
leur intersection - ou de leur direction si elles sont
parallèles, sont P (ab", b'a",
b"a").
De même on trouve N(ac', a'c',
c"a') et M (bc, b'c, c"b).
Ainsi, les trois "points" sont "alignés", (au
sens rappelé dans les illustrations) ssi D, le
déterminant de leurs coordonnées, est
nul.
|
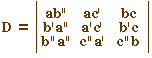
|
Conditions pour que A', B', C' soient sur
une conique passant par A, B, et C
Les trois réels u,
v et w
doivent vérifier le système en inconnues
U, V, W
:
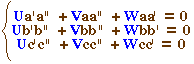
|
Soit alors 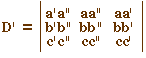
|
Les points A', B', C' seront sur une conique passant par A, B et
C ssi ce système homogène admet une solution non
triviale, et donc que ce n'est pas un système de Cramer, soit
encore ssi D' = 0.
Equivalence des deux
condtitions
Le calcul, par exemple par la formule de Sarrus, montre que les
deux déterminants sont formellement identiques. La
nullité de D est donc équivalente à celle de
D'.
Unicité de la conique ainsi
trouvée
Le déterminant D est nécessairement de rang 2. S'il
était de rang 1, les trois points M, N et P seraient
confondus. Or, par exemple, M = N conduit à A, B, C
alignés, et c'est par hypothèse un repère
affine. Comme D = D', D' est aussi de rang 2, donc les solutions
effectives (u, v, w) du système sont proportionnelles: elles
définissent la même conique.
Illustrations - Preuve
- Consèquences
Conséquences -
Extension
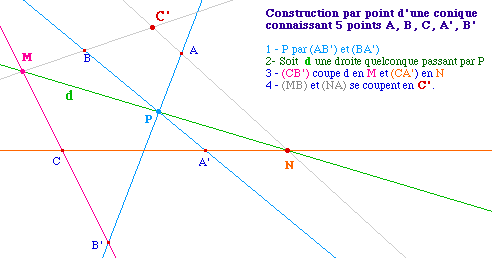
L'item Conique de Cabri : Tracé
d'une conique connaissant 5 points
Si on connaît 5 points A, B, C, A' et B', d'une conique, on
peut utiliser le théorème de Pascal pour en construire
un sixième :
|
|
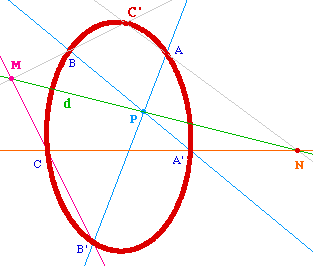
En faisant tourner la droite d autour de P, on obtient
ainsi une génération par point d'une conique
à partir de 5 de ces points, et cette construction
permet de conclure que par 5 points dont 3 ne sont pas
alignés, il passe une unique conique.
 Pascal06.fig
Pascal06.fig
|
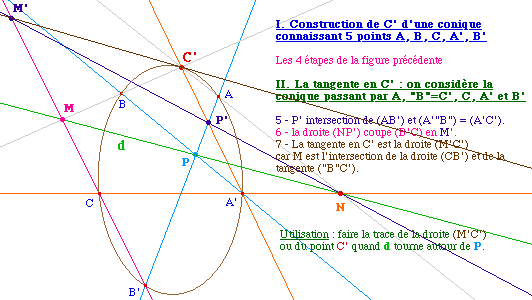
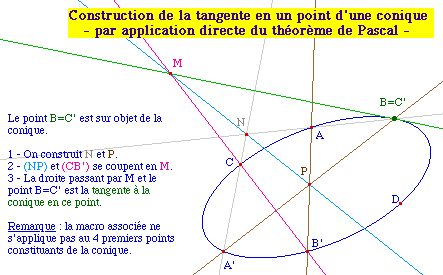
Le cas où deux points sont confondus
: construction de la tangente en un point d'une
Cabri-conique
On peut affiner les hypothèses du théorème
de Pascal puisque quand nous disons "... dont 3 ne sont pas
alignés", nous avons besoin seulement de savoir que la conique
est non impropre - ou non dégénérée. Mais
on peut faire la même preuve en supposant que deux points - par
exemple B et C' - sont confondus. Cette information se traduisant
alors par la donnée de la tangente en C' à la conique.
Ainsi, on peut construire à la règle et au compas,
à partir de 5 points d'une conique, non seulement un
sixième point C', mais aussi la tangente à la conique
en ce point.
 Pascal07.fig
Pascal07.fig
Une autre façon de voir la situation - peut-être
plus simple pour une première lecture - est de
considérer 4 points d'une conique, alors la tangente en un
cinquième point, connu comme étant sur la conique est
facilement constructible comme ci-dessous :
 PasApp02.fig ou TgSurCnk.mac
PasApp02.fig ou TgSurCnk.mac
Illustrations - Preuve
- Consèquences
[I.1 - Introduction et
exemples] [I.3 -
Applications du théorème de Pascal]
[I.4 - Théorème de
Carnot par les coordonnées barycentriques]
[Retour "Considérations
affines et projectives"] [Retour
Coniques]
 Menu
général
Menu
général

![]() Pascal04.fig (Cas de la parabole)
Pascal04.fig (Cas de la parabole)