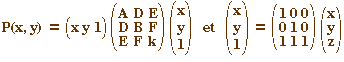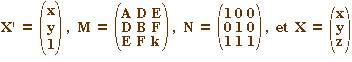Coniques en
coordonnées barycentriques
I.1 - Introduction - Exemples des
ellipses de Steiner
[I.2 - Théorème de
Pascal] [I.3 - Applications
du théorème de Pascal]
[I.4 - Théorème de
Carnot par les coordonnées barycentriques]
[Retour "Considérations
affines et projectives"] [Retour
Coniques] [Menu
Général]
Rappel : Soit ABC un (vrai) triangle, (A,
B, C) est un repère affine. Ma pour coordonnées
homogènes (x, y ,z) dans ce repère s'écrit M =
xA +y B +zC avec x+y+z = 1. C'est équivalent à
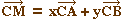 ,
c'est-à-dire M(x, y) dans le repère cartésien
,
c'est-à-dire M(x, y) dans le repère cartésien
 -
le point associé à la composante "z" devenant
l'origine.
-
le point associé à la composante "z" devenant
l'origine.
Exemple des ellipses de Steiner
Equations barycentriques d'une conique et
de ses tangentes.
Considèrons un polynôme du second degré en x
et y de la forme
P(x, y) = Ax2
+By2 +2Dxy + 2Ex + 2Fy + k (avec l'un des trois termes
A, B ou D, au moins, différent de 0)
L'ensemble C des points M(x, y) dans
un repère cartésien donné, tels que P(x, y) = 0,
est appelé une conique du plan,
d'équation P(x, y) = 0.
La transformation qui, aux coordonnées cartésiennes
(x, y), associent celles barycentriques (x, y, z = 1-x-y) donne la
forme des équations barycentriques des coniques : ce sont des
polynômes homogènes du second
degré, de la forme F(x, y, z) = 0 avec
F(x, y, z) = ax2 +
by2 + cz2 + 2a'yz + 2b'zx + 2c'xy =
0.
Pratiquement on passe de la première à la seconde
en remplaçant les termes du premier de degré et le
terme constant en terme du seconde degré, en multipliant par 1
= (x+y+z). On peut aussi avoir un regard matriciel (proposé
par Tisseron) :
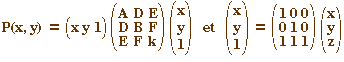
En notant 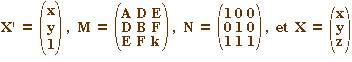
P(x, y) = tX'MX', soit F(x, y, z) =
tXtNMNX, soit, en posant A = tNMN,
on a F(x, y, z) = tXAX.
De même, la tangente en un point
M0(x0, y0, z0) à
cette conique a pour équation barycentrique :
(ax0 + c'y0 +
b'z0)x + (by0 + a'z0 +
c'x0)y + (cz0 + b'x0 +
a'y0)z = 0,
relation que l'on obtient à partir de l'équation
cartésienne de la tangente en M0 à la
conique d'équation P(x, y) = 0, soit :
Axx0 +
Byy0 + D(xx0 +yy0) + E(x +
x0 ) + F(y + y0) + k = 0.
Cas particulier d'une conique passant par
les points du repère affine.
On suppose que la conique passe par les points A, B et C du
repère affine. Alors F(1, 0, 0) = 0 entraine a=0, de
même F(0, 1, 0) = 0 entraine b = 0 et F(0, 0, 1) entraine c =
0.
L'équation barycentrique, dans un repère affine (A,
B, C) d'une conique passant par ces trois points est de la forme
a'yz + b'zx + c'xy = 0.
Cas particulier des coniques
impropres.
Soit une conique impropre - ayant au moins trois points - dont
trois points distincts A, B et C sont alignés. Alors cette
conique est la réunion de deux droites (éventuellement
confondues).
En effet, Plaçons nous dans un repère affine (A, B,
D), avec D n'appartenant pas à la droite (AB). Et soient (u,
v, 0) les coordonnées barycentriques de C dans (A, B, D). Par
la même démarche que ci-dessus, on a d'une part a=0 et b
= 0 (par A et B sur la conique) et d'autre part c' = 0 (par C est sur
la conique).
L'équation de la conique devient
cz2 + 2a'yz + 2b'zx = 0, soit
encore z(cz + 2a'y + 2b'x) = 0.
La conique est donc la réunion de deux droites
d'équation barycentrique:
z = 0 (c'est la droite
(AB) et
cz + 2a'y + 2b'x = 0 qui peut
être sécante, strictement parallèle ou
confondue avec la droite (AB).
Par exemple la conique impropre formée de la
réunion :
des deux droites (AB) et (AC) est d'équation
barycentrique yz = 0.
de la droite (AB) et de la parallèle à (AB)
passant par C est d'équation barycentrique
xz + yz = 0.
des médianes (AA') et (BB') de ABC est
d'équation barycentrique :
z2 + xy - xz - yz =
0.
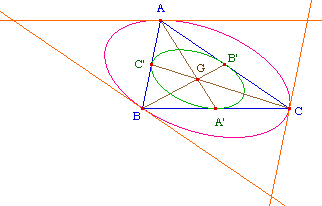
Exemple des ellipses de
Steiner.
La conique inscrite est tri-tangente au triangle ABC en les
milieux des côtés. Celle circonscrite passe par les
sommets et a sa tangente en chaque sommet parallèle au
côté opposé du triangle.
 Steiner2.fig
Steiner2.fig
L'ellipse circonscrite
Son équation est de la forme a'yz +
b'zx + c'xy = 0. En écrivant que la parallèle
à (BC) en A - d'équation barycentrique
y + z = 0 - est tangente à la
conique, il vient c'y + b'z = 0, soit
donc c' = b'. En écrivant l'équation d'une autre
tangente, par exemple en B, il vient c' = a'.
Ainsi une équation barycentrique est donc
xy + yz + zx = 0.
Remarque : on a montré en même
temps que la conique passant par A, B, C, ayant pour tangente en A la
parallèle à (BC) et pour tangente en B la
parallèle à (AC) a nécessairement pour tangente
en C la parallèle à (AB).
L'ellipse inscrite
Soient A', B', C' les milieux des côtés
opposés à A, B et C respectivement. La conique passant
par le point A' donne a+b+c' =0. De même, le fait qu'elle passe
par B' et C' aboutit à b+c+a' =0 et c+a+b' = 0.
Par ailleurs, la conique en A', d'équation (c'+b')x + (2b
+ a')y + (2c + a')z = 0, devant être la droite (BC)
d'équation x = 0, donne a' = - 2b = -2 c et donc b = c. De
même l'équation de la tangente en B' étant la
droite (AC) aboutit à c = a.
L'équation de l'ellipse de Steiner inscrite est donc
x2 + y2 + z2 -
2xy - 2yz - 2zx = 0.
Remarque : comme ci-dessus, on a
montré par la même occasion que la conique passant par
A', B', C', les milieux des côtés opposés
à A, B, C et ayant pour tangente en A' la droite (BC) et pour
tangente en B' la droite (AC) a nécessairement pour tangente
en C' la droite (AB).
Haut
Notes : Ces deux coniques ont pour centre le centre de
gravité G du triangle, elles sont homothètiques
(hG,2). D'un point de vue euclidien celle inscrite est
l'ellipse d'aire maximale inscrite dans le triangle, celle
circonscrite est l'ellipse d'aire minimale circonscrite au
triangle.
[I.2 -
Théorème de Pascal] [I.3
- Applications du théorème de Pascal]
[I.4 - Théorème de
Carnot par les coordonnées barycentriques]
[Retour "Considérations
affines et projectives"] [Retour
Coniques] [Menu
Général]
 Menu
général
Menu
général