Une preuve du théorème de Carnot a été proposé dans une approche "cercle + homologie harmonique" qui ne relève pas vraiment du programme de CAPES. Nous proposons ici une preuve directement accessible avec l'outil "Barycentre".

Notations du théorème de base

 

Théorème de Carnot à montrer Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets. Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi :

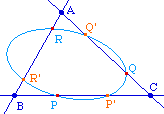
Notation utilisée pour cette preuve : on se place dans le repère affine (A, B, C). Posons P (0, 1, -p), P' (0, -p', 1) ce qui signifie que
De même, on pose Q (-q, 0, 1) et Q' (1, 0, -q') puis R (1, -r, 0) et R'(-r', 1, 0), ce qui induit des relations analogues entre les coordonnées barycentriques et les rapports de mesures algébriques.

Avec ces notations, le théorème de Carnot s'écrit : les 6 points sont sur une conique ssi

Remarque : avec ces notations P et P' sont confondus ssi pp' = 1.

 

Dans toute la suite, l'équation générique de la conique étudiée E, dans le repère affine (A, B, C), sera notée

ax² + by² + cz² + 2a'yz + 2b'zx + 2c'xy = 0.

Rappelons que la tangente en un point M₀(x₀, y₀, z₀) a pour équation barycentrique

(ax₀ + c'y₀ + b'z₀)x + (by₀ + a'z₀ + c'x₀)y + (cz₀ + b'x₀ + a'y₀)z = 0

En fait, pour cette approche barycentrqiue, seul le sens direct (6 points sur une conique entraine la relation de Carnot) nous intéresse. En effet, la réciproque se fait classiquement par la méthode des coïncidences comme elle est déjà proposée dans l'autre contexte.

Preuve du théorème

Cas où les points sur chaque coté du triangle sont distincts.

Ainsi nous somme dans le cas où les produits pp', qq' et rr' sont tous différents de 1.

Puisque les trois produits (1-pp'), (1-qq') et (1-rr') ne sont pas nuls, les relations d'appartenance des points pris deux à deux entrainent, respectivement, bp' = cp, cq' = aq, et ar'=br.

Une droite (en particulier les côtés du triangle) ne coupant pas une conique en trois points, la conique cherchée ne passe par aucun sommet du triangle, le produit abc est non nul. En multipliant les trois égalités terme à terme, il reste donc pqr = p'q'r' ce que l'on voulait montrer.

Cas où les points d'un côté du triangle sont confondus.

Plaçons nous dans le cas où P = P'. Cela signifie que la droite (BC) coupe la conique en un point double, elle est donc tangente à la conique en P. La droite (BC) est d'équation x=0. Que cette droite soit la tangente en P aboutit au système b - a'p = 0, -cp + a' = 0. Ce qui aboutit à b = cp². C'est donc la même relation que bp' = cp puisque p' = 1/p dans ce cas.

Ainsi la relation pqr = p'q'r' est vraie même si sur une droite deux points sont confondus.

Cas des coniques tri-tangentes

En reprenant la même démarche que ci-dessus, on arrive à :

En faisant le produit terme à terme on arrive au système c = aq², b = aq²p², a = ar²q²p². Si r²q²p² est différent de 1, il vient a=0, b=0, c=0 et donc a'=0, b'=0, c'=0 : il n'y a pas de conique.

Donc r²q²p² =1 soit pqr = 1 ou pqr = -1.

Cas où pqr = 1 (c'est-à-dire - par Ménélaüs - P, Q, R alignés)

Le système devient c = aq² et b = aq²p². Il y a une unique conique solution, elle est d'équation :

x² + q²p² y² + q² z² + 2pq²yz + 2qzx + 2pqxy = 0 ou encore (x + pqy + qz)²=0

On trouve la droite "double" PQR. Réciproquement, cette droite ne convient pas.

Cas où pqr = -1 (c'est-à-dire - par Céva - (AP), (BQ) et (CR) concourantes ou parallèles)

Le système s'écrit tujours c = aq² et b = aq²p². Il y a une unique conique solution, elle est d'équation :

x² + q²p² y² + q² z² + 2pq²yz + 2qzx - 2pqxy = 0 (seule différence : le signe du dernier terme)

Conclusion   Soient ABC un triangle, P, Q, R sur les côtés (BC), (CA), et (AB). Il existe une conique tri-tangente au triangle en P, Q et R si et seulement si les trois céviennes (AP), (BQ) et (CR) sont concourantes ou parallèles.   Utiliz01.fig (pour la macro de construction de la conique)

Nature de cette conique

En revenant au repère cartésien la conique a pour équation :

(1-q)²x² + q²(1-p)²y² - 2q(pq+1- q)xy + 2q(1-q)x - 2q²(1-p)y + q² = 0.

On peut simplifier les calculs en se plaçant dans le repère .

M = XQ + YP + (1-X-Y)C = = xA + yB + (1-x-y)C

D'où les formules de changement de repère :

On obtient la nouvelle équation : X² + Y² + 2kXY - 2X - 2Y + 1 = 0 avec ce qui peut aussi s'écrire :

(X+kY-1)² +(1-k²)Y² - 2(1-k)Y = 0 avec

Ce qui permet de discuter la nature de la conique :

Exemple d'illustration sur la parabole : p = (q-1)/q

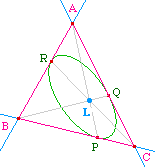
Choisissons q = -1, c'est-à-dire Q miliueu de [AC], Q = (A+C)/2, on a p = 2 soit P = 2C - B, et choissisons R tel que (AP), (BQ), (CR) soient concourantes. On peut obtenir la conique par la macro Cnk1P2TC.mac qui la construit à partir de 2 tangentes, leurs contacts et un point en l'appliquant à R, (AC), Q, (BC), P. On retrouve, pour la parabole, une configuration bien connue, spécifique de ses propriétés affines. CarnotP1.fig

Compléments sur les paraboles par cette méthode (propriétés du point L)

Menu général