[4 - Liens sur ce sujet] [Retour Algébre] [Menu général]
Présentation | Ellipse | Hyperbole | Parabole | Commentaire
Dans la première page, la structure de groupe sur la conique provient de la théorie générale des groupes sur une cubique. Il est construit en adjoignant à une conique affine une droite affine. On a donc une cubique. D'un point de vue projectif, il n'y a qu'un seul type de conique. Et ainsi en adjoignant une droite, on dispose d'un seul type de cubique, et donc d'une seule structure de groupe.
Mais on peut aussi s'intéresser à un point de vue affine. On dispose alors de trois types de coniques, et chacune étant bien particulière correspond alors à un groupe bien particulier. Nous allons dans cette page construire successivement :
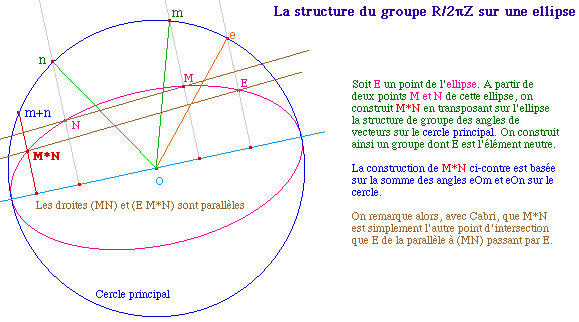
- Un groupe sur une ellipse, isomorphe à (R/2piZ, +), et plus précisément, le groupe des angles.- Un groupe sur une hyperbole, isomorphe à (R*, x) comme dans la page sur l'équation de Pell-Fermat.
- Un groupe sur la parabole, isomorphe à (R, +)
Ainsi, comme il est naturel de la penser, d'un point de vue affine, l'ellipse, l'hyperbole et la parabole sont respectivement isomorphes, avec transfert de structure, au cercle, à la droite réelle privée d'un point et à la droite réelle.
Puis une fois fait ce travail, nous nous apercevrons, grâce à Cabri, que nous avons fait trois fois la même chose, dans le plan projectif ...

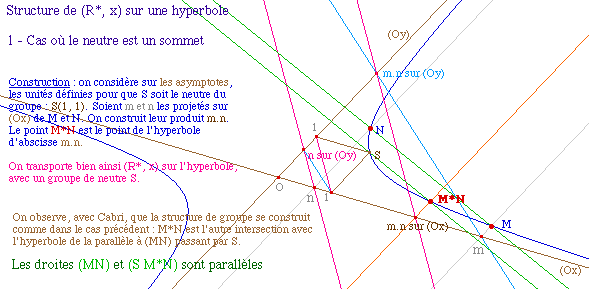
Un premier cas particulier
Cas général
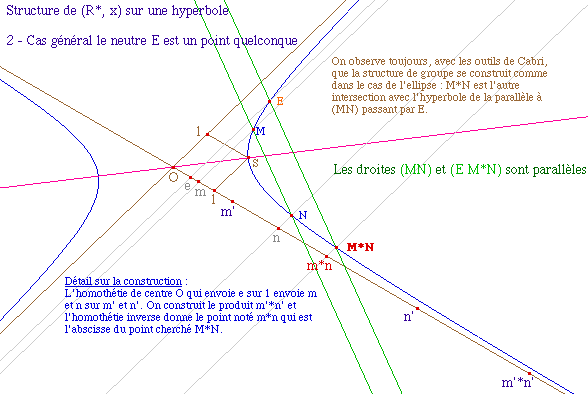
GrpHyp2.fig
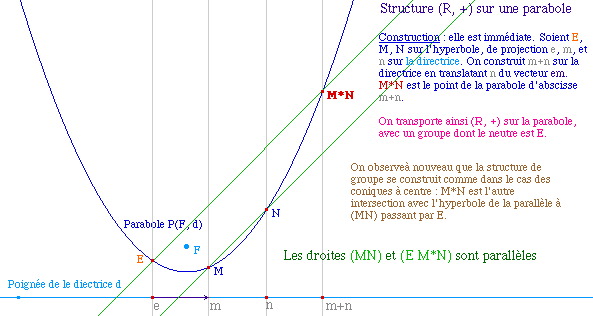
Utilisation pédagogique
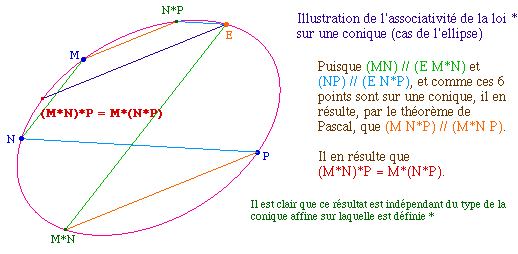
Dans le cadre d'un cours de géométrie affine, aprés le théorème de Pascal, on peut, dans un TP, envisager cette loi de composition, montrer qu'elle induit un groupe. Considérant cette loi où M*N est le second point de la parallèle à (MN) passant par E. Il est clair que la loi est commutative, que E est neutre. On construit aisément l'inverse d'un point. Reste l'associativité qui est - encore une fois - une conséquence du théorème de Pascal.
GrpEll02.fig
Il s'agirait surtout ensuite de faire chercher les groupes isomorphes correspondant à chaque conique. C'est immédiat pour la parabole - ou presque - demande d'être un peu guidé par l'ellipse, et nécessite peut-être quelques questions intermédiaires pour l'hyperbole.
Si un enseignant ou formateur rédige un tel TP ... merci d'en faire profiter abraCAdaBRI
Le groupe projectif associé
Par rapport à la structure de groupe sur une ellipse comme proposé dans le sujet du CAPES interne 91, la seule différence est que la droite affine du sujet est remplacée par la droite à l'infini. En effet si on note encore L l'intersection de la droite (MN) avec la droite à l'infini, tracer (EL) revient, dans le plan affine, à tracer la parallèle à (MN) passant par E.
Autrement dit, la théorie générale, dans le plan projectif, d'une structure de groupe sur une cubique, appliquée à une conique et la droite projective à l'infini permet de retrouver, sur les coniques affines, à partir d'un groupe unique projectif, les trois groupes fondamentaux de l'analyse :
it avoir Parabole Hyperbole (R/2piZ, +) (R, +) (R*, x) Remarque avancée
Un collaborateur actif - et avisé - d'abraCAdaBRI, Dominique Tournès, nous communique un extrait du livre de Yves Hellegouarch, Invitation aux mathématiques de Fermat-Wiles, Masson, p. 199, qui semble de nature à expliquer le phénomène :
"Lorsque C est singulière, on désigne par C0(k) l'ensemble des points non singuliers de C dans P2(k). Alors si O appartient à C0(k), la construction ci-dessus permet de munir C0(k) d'une loi de groupe abélien (...).
Lorsque le point singulier de C est un point de rebroussement, C0(k) est isomorphe au groupe (k,+).
Lorsque le point singulier de C est un point à tangentes distinctes dans P2(k), C0(k) est isomorphe à (k*,x)."Est-ce qu'un lecteur d'abraCAdaBRI serait en mesure de nous apporter des précisions sur ces théorèmes, et de nous expliquer en quoi la parabole et l'hyperbole rentrent bien dans ce cadre ?
Exercice en guise de conclusion partielle
Si le webmestre a un peu compris la remarque précédente - si ... - pour illustrer ce complément théorique de Dominique Tournès, on peut s'essayer à retrouver, dans le cas du groupe de la page 1 (du CAPES interne 91), (R, +) en prenant la droite auxiliaire tangente à la conique, et (R*, x) en la prenant sécante à la conique.
Présentation | Ellipse | Hyperbole | Parabole | Commentaire