
Cette page trouve - elle aussi - son origine dans le sujet de CAPES interne 1991. Dans la première partie de ce sujet, on cherche à résoudre dans Z l'équation x2 - 3y2 = 1. La suite est à prendre comme une simple illustration graphique de cette partie.
Comme utilisateur régulier de Cabri, je suis toujours impressionné de la précision du logiciel. Par exemple ici, ce qui m'a fasciné - et ce que j'ai voulu mettre en ligne - c'est la capacité de Cabri à retrouver les valeurs entières - exactes - des premiers couples solutions de cette équation de Pell-Fermat.
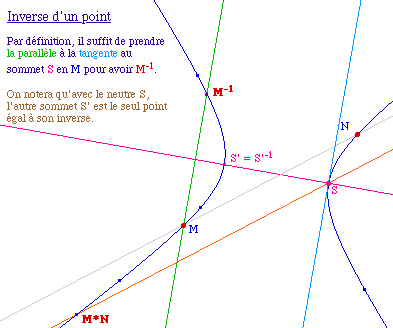
Définition de la loi de composition

GrpHyp01.fig ou LoiHyp.mac
La preuve dans le sujet de CAPES
Elle est basée sur du calcul dans un repère lié aux asymptotes. On montre alors assez rapidement que (H, *) est ismorphe au groupe multiplicatif des nombres réels non nuls (R*, x).
Preuve géométrique par le théorème de Pascal (non présente dans le sujet)


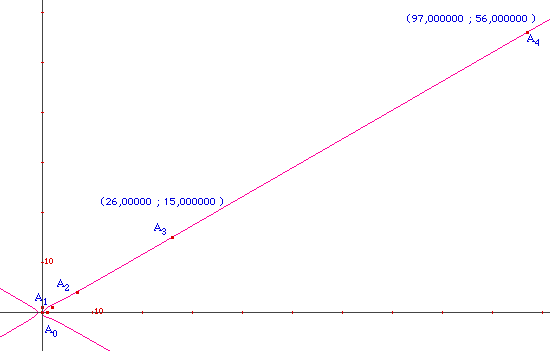
On peut apprécier la
précision de Cabri dans son calcul de coordonnées,
sur une hyperbole, avec un repère d'un pixel ...
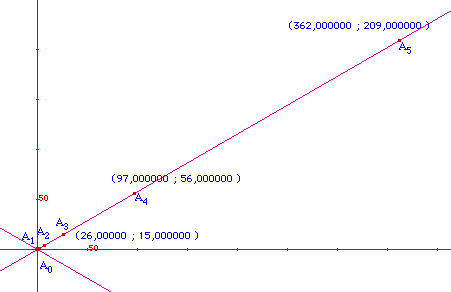
Y-a-t-il un procédé géométrique simple pour passer des solutions ainsi trouvée à x2 - ay2 = 1 aux solutions de x2 - ay2 = -1 sur l'hyperbole conjuguée ?
Merci d'envoyer vos commentaires à abraCAdaBRI.
D'une manière générale, si vous avez des suggestions pour compléter cette page, n'hésitez pas à les proposer ...
Si le sujet vous intéresse, il peut être intéressant de voir la page - ci-dessous - sur les autres groupes sur une conique. Le résultat est assez passionnant ...