
[4 - Liens sur ce sujet] [Retour Algébre] [Menu général]

Dans la suite, on suppose la relation algébrique connue. Il resterait à montrer qu'elle correspond effectivement à la construction géométrique. C'était une partie de l'activité de calcul symbolique sur la TI 92 que nous ne reproduisons pas ici.
Position du problème
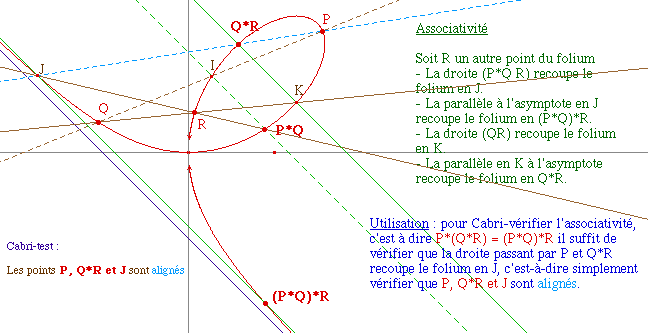
Preuve du résultat
Compte tenu de la relation algébrique, l'associativité résulte de celle des nombres réels. Si P, Q et R ont pour paramètre respectif p, q et r, Q*R a pour paramètre -qr et donc P*(Q*R) a pour paramètre pqr. De même P*Q a pour paramètre -pq et (P*Q)*R a bien pour paramètre pqr.
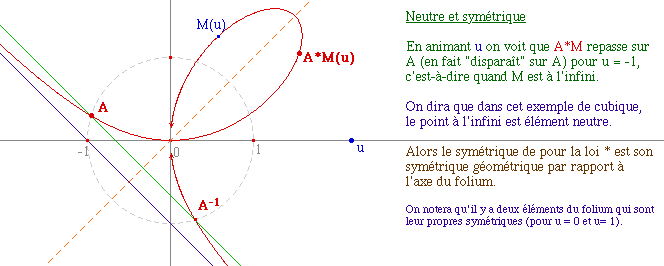
L'élément neutre est le point à l'infini dans la direction de l'asymptote. On se place alors, de fait, dans le plan projectif pour étudier la structure de groupe. C'est une situation générale sur les cubiques (ou les courbes elliptiques).
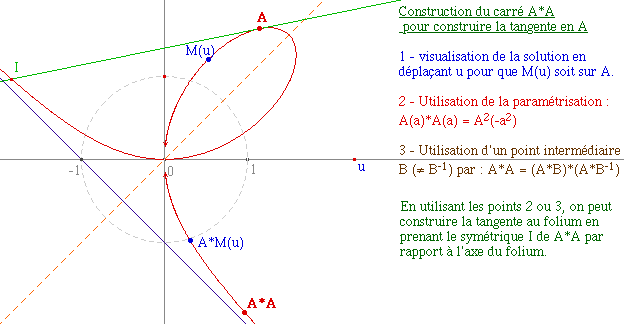
Autre exemple de structure de groupe sur une cubique : lors du colloque sur l'histoire des Mathématiques organisé par l'IUFM de La Réunion en novembre 97, DominiqueTournès a présenté, dans un atelier, un travail de Ramajunan sur les nombres sommes de deux cubes à partir d'une structure de groupe sur une cubique.
Télécharger l'article au format .pdf - 56 Ko (se rendre sur le site pour le format Postscript 3.3 Mo)