Paraboles passant par 4 points

 

[1 - Préliminaires] [2 - Généralités sur les coniques] [3 - Coniques comme homologue harmonique d'un cercle] [4 - Point de Frégier]
[5 - Applications du point de Frégier] [6 - Diverses déterminations des foyers] [7 - Tangentes communes à deux coniques]
[8 - Normales à une conique issue d'un point] [Retour Présentation de la conférence] [Accueil Coniques]

 

Etant donnés quatres points A, B, C, D du plan, on se propose de construire les paraboles passant par ces 4 points.

Une première remarque : puisque l'intérieur d'une parabole est convexe, il faut que le quadrilatère formé par ces 4 points soit lui aussi convexe.


Combien de paraboles par 4 points ? Une approche expérimentale

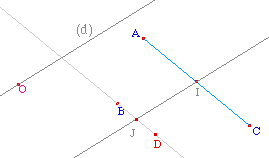
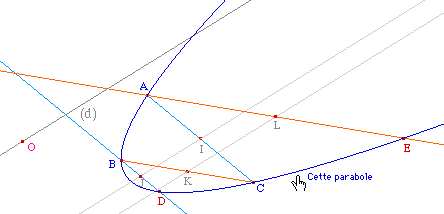
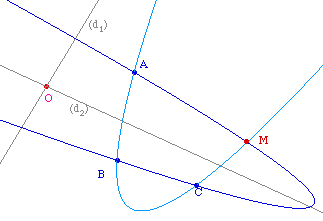
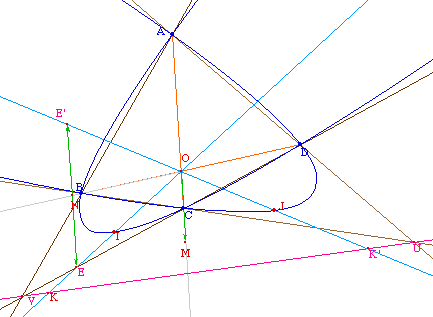
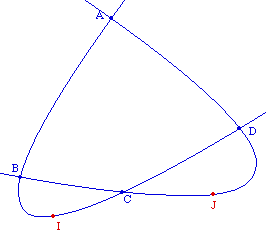
En pensant à la représentation graphique d'une équation du second degrè, il est clair que par trois points il ne passe qu'une seule parabole ayant une direction d'axe donnée.

Pour cette approche expérimentale dans Cabri II, nous proposons l'appareillage suivant : une droite (éventuellement plusieurs) tourne autour d'un point fixe O. Trois points A, B, C étant donnés de base, on construit la parabole passant par ces trois points et d'axe parallèle à la droite tournante (d). En ajoutant un quatrième point, et en faisant tourner (d), on observe combien de paraboles passent en général par les quatre points.

Para4F2.fig

Propriété utilisée

Etant donnée une corde [AC] d'une parabole. La parallèle à l'axe de la parabole passant par le milieu I de cette corde est axe d'une symétrie oblique laissant globalement invariante la parabole, la direction de cette symétrie étant celle de la corde [AC] : on construit ainsi un point D de la parabole, par symétrie oblique.

On recommence pour avoir un cinquième point E de cette parabole d'axe parallèle à (d).

La macro TestPara.mac qui, étant donnés trois points A, B, C, une droite (d), construit la parabole passant par A, B, C et d'axe parallèle à la droite.

 

Visualisation expérimentale des paraboles solutions

Cette macro étant disponible, on peut maintenant, à partir de trois points données A, B, C, d'un point M, et d'une droite (d) pivotant autour d'un point O, observer le nombre de paraboles passant par 4 points.
Puisque que l'on en trouve deux, il est intéressant de tracer deux droites passant par O et d'appliquer deux fois la macro précédente.

ParaTest.fig

 

Construction des deux paraboles passant par 4 points

 

La construction suivante est proposée par Michel Guillerault

 

Préliminaire : une macro Moyenne géométrique

O est un point sur objet du segment [MN], on veut, à partir de O, construire un point U (Moy sur la figure) de la demi-droite [ON) tel que OU soit moyenne géométrique de OM et ON, c'est-à-dire U tel que OU2=OM.ON.
Pour cela, on trace le cercle de diamètre [AB], et on utilise les relations métriques du triangle rectangle, sur la hauteur, OI2=OM.ON que l'on reporte sur la demi-droite voulue.

La figure MoyGeo.fig ou La macro MoyGeo.mac pour construire la suite.

L'idée est bien-sûr de construire un cinquième point de chacune des deux paraboles pour pouvoir construire une Cabri-parabole.

Etape 1

 

On commence par construire O l'intersection des diagonales [AC] et [BD]. On notera que l'existence de O assure que le quadrilatère est convexe, et donc qu'il y a des solutions. On applique la macro précédente pour construire M sur la demi-droite [OC) et N sur la demi-droite [OB) tels que OM2=OA.OC et ON2=OD.OB, puis on construit, par translation, les parallélogrammes OMEN et OMNE'.

Un premier résultat est que les axes des paraboles solutions sont parallèles à (OE) et (OE').

Etape 2

Soient U l'intersection des droites (BC) et (AD) et V celle des droites (AB) et (CD). La droite (UV) coupe (OE) en K et (OE') en K'. Alors les milieux I de [OK] et J de [OK'] sont des cinquièmes points de chacune des deux paraboles cherchées.


La figure Para4pts.fig


La macro Para4pts.mac qui, étant donnés A, B, C, D, construit les deux paraboles passant par ces quatre points.

Preuve

Michel Guillerault a bien entendu fourni une preuve de la construction proposée. Mais abraCAdaBRI est encore bien jeune, on lui pardonnera pour cette fois : promis, il ne fera plus des caprices de gamin en demandant aux artistes réalisés "dis, M'sieur, dessine moi une parabole passant par 4 points".

Texte original (pour les autres artistes) : il suffit d'écrire l'équation générale des coniques passant par 4 points (faisceau linéaire de coniques) et d'imposer ensuite à ces coniques d'être des paraboles. Ici, on a choisi (OA) et (OB) comme axe.

 

Note : Dans la partie "Par type" du dossier sur les coniques, abraCAdaBRI proposera une construction, basées sur des exercices de notre référence "Lebossé et Hémery", utilisant un point de vue et des résultats géométriques plus élémentaires.

 

Un cas particulier intéressant

 

C'est le cas où les 4 points A, B, C, D sont cocycliques.

 

Alors dans ce cas les axes des deux paraboles sont orthogonaux, et de plus ils sont sécants à l'isobarycentre des 4 points.

La figure Para4Ccl.fig

 

[1 - Préliminaires] [2 - Généralités sur les coniques] [3 - Coniques comme homologue harmonique d'un cercle] [4 - Point de Frégier]
[5 - Applications du point de Frégier] [6 - Diverses déterminations des foyers] [7 - Tangentes communes à deux coniques]
[8 - Normales à une conique issue d'un point] [Retour Présentation de la conférence] [Accueil Coniques]


Menu général