Université d'été 96

Extraits de la conférence de Michel Guillerault

7 - Constructions spécifiques à Cabri II
Tangentes communes à deux coniques

Préambule

Dans cette page et la suivante, nous nous proposons maintenant d'explorer l'une des possibilités spécifiques de Cabri II en ce qu'il permet de construire l'intersection de deux coniques : par rapport aux pages précédentes, nous quittons désormais la géoémtrie de la règle et du compas puisque l'on aborde, sur le plan analytique, des problèmes d'ordre 4 dont on sait qu'ils sont - sauf cas particuliers - inacessibles à la règle et au compas.

Pour ce qui est des tangentes communes à deux coniques (C) et (C'), nous allons nous ramener à l'intersection de (C) avec une conique (C") transformée de la première par polaires réciproques par rapport à (C), transformation qui sera explicitée plus loin.

Conique définie tangentiellement

Cabri permet la construction d'une conique définie par 5 points. Pour travailler par polaires réciproques, il faut pouvoir disposer de coniques définies par 5 tangentes, et donc, pour les utiliser avec Cabri, de les construire comme définies par 5 points. Pour cela, il suffit de savoir construire les points de contact avec les cinq tangentes.

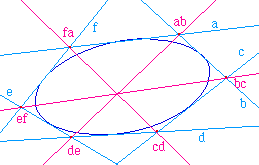
	Pour trouver ces points de contact sur les tangentes, on utilise le théorème de Brianchon : Soient 6 droites a, b, c, d, e, f tangentes à une conique. Si on note ab, bc, cd, ce, ef et fa les intersections des droites a et b, puis b et c, etc, les trois droites passant par ab, de, puis bc, ef et par cd, fa sont concourantes. Même si cela ne sert pas pour la suite, on peut choisir de Lancer la figure Brianchon.fig
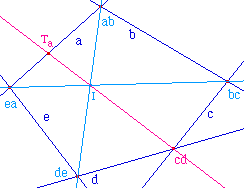
	Plus précisément, ce qui va nous intéresser ici, c'est le cas particulier où f=a. On a alors 5 tangentes et le point fa est le point de contact de la tangente a à la conique. En pratique, on trace l'intersection des droites (ab, de) et (bc, ea). La droite passant par ce point et cd coupe la droite a en un point Ta qui est le point de contact de la tangente a à la conique.
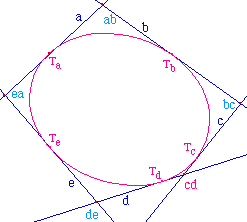
	On transforme ensuite cette construction en une macro pour l'appliquer aux 4 autres droites successivement, ce qui permet de construire dans Cabri II la conique définie tangentiellement par 5 tangentes.   La figure CDefTgt2.fig La macro Conique définie tangentiellement (fichier CDefTgte.mac, nécessaire pour réaliser les figures suivantes)

Transformation par polaires réciproques

Contexte

La transformation par polaires réciproques par rapport à une conique (C) est une bijection de l'ensemble des points et des droites du plan projectif - le plan "usuel" muni d'une droite supplémentaire dite "droite de l'infini" - sur l'ensemble des points et des droites du plan projectif, qui, à chaque point P fait correspondre sa polaire (p) par rapport à la conique (C) et qui à chaque droite (d) fait correspondre son pôle D par apport à la conique (C).

Ainsi, la conique (C) elle-même, considérée comme ensemble de points - donc définie ponctuellement - est transformée en l'ensemble de ses tangentes. On décide d'identifier cet ensemble de tangentes à une conique définie tangentiellement, identifiable finalement à (C) elle-même.

La transformation par polaires réciproques fait donc correspondre à un point une droite, à une droite un point, à une conique définie ponctuellement une conique définie tangentiellement, à une conique définie tangentiellement une conique définie ponctuellement, soit à une conique une conique.

Réalisation d'une macro Transformée par polaires réciproques

Pour faire les figures suivantes, vous aurez besoin, outre de la macro précédente sur la définition tangentielle des coniques, de :

Charger les macros Polaire d'un point et Tangente en un point d'une conique

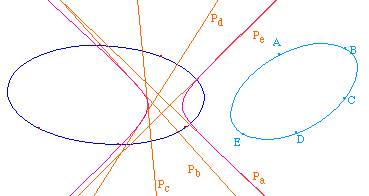
Pour transformer la conique (C') - en bleu clair - par polaire réciproque par rapport à la conique (C) - en bleu foncé - on commence par prendre la polaire des 5 points constituants A, B, C, D, E par rapport à (C). On obtient ainsi 5 tangentes, donc une conique définie tangentiellement, que l'on transforme en conique (C") définie ponctuellement par la macro réalisée au paragraphe précédent. La figure TrPPol.fig La macro Transformation par polaires réciproques (fichier TrPPolRe.mac)

Construction des tangentes communes

Cabri II nous permet de construire l'intersection de la conique (C) et de la transformée (C") de (C') - seule partie non constructible à la règle et au compas. Ces points d'intersection sont les points de contact, sur (C) des tangentes communes à (C) et (C'). En effet, un tel point, étant un point de (C), dans la transformée par polaires réciproques par rapport à (C) est transformé en la tangente à (C) en ce point, et comme point de (C") il est transformé aussi en une tangente à (C') : les tangentes à (C) en ces points sont aussi tangentes à (C').

La figure Tgt2Cn.fig, ou La macro Tangentes communes à deux coniques (fichier Tg2Conik.mac)

Surcharge de la macro Tangente commune à deux coniques

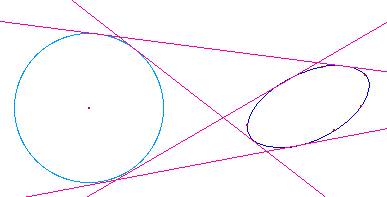
Une fois la macro réalisée, il peut être intéressant de la surcharger par une tangente à un cercle et une conique.   Pour cela on prend un cercle et une conique, on construit sur le cercle une ellipse circulaire et on applique la macro précédente au cercle et à la conique (de façon que ce soit l'ellipse circulaire qui soit la transformée, sinon il peut y avoir quelques difficultés selon la façon dont on a construit l'ellipse circulaire). Puis on surcharge la macro précédente en donnant la possibilité d'avoir un cercle comme objet initial.

La figure TgteCeCo.fig   La macro Surchargée du cercle (fichier Tgt2CnSu.mac)

Menu général