Université d'été 96

Extraits de la conférence de Michel Guillerault

4 - Le point de Frégier

Le point de Frégier

 Considérons l'homologue d'un cercle dans une homologie de centre un point A de ce cercle. On a déjà dit que la conique image passe aussi par A en y étant tangente au cercle.

Comme toutes les droites passant par A sont globalement invariantes, deux droites orthogonales (MA) et (NA) coupant le cercle en M et N coupent la coniques en leurs images M' et N'. Comme (MN) passe par le point fixe O, toutes les droites images (M'N') passent aussi par un point fixe F, image de O dans l'homologie de centre A, d'axe (d). Ce point F s'appelle le point de Frégier associé au point A : c'est donc le point commun à toutes les cordes de la conique vues de A sous un angle droit. Puisque F est sur la droite (OA), (FA) est la normale à la conique en A, ce qui donne une autre possibilité de construction de tangente en un point, par la normale. PtFregier.fig

On notera en particulier que cette possibilité est intéressante pour tracer une tangente en un point d'une parabole, comme cela a été utilisé à la page précécente.

Construction du point de Frégier

Puisque c'est le point commun à toutes les cordes vue du point M sous un angle droit, il suffit d'en construire deux à partir des points constituants de la conique. La macro Fregier.mac d'objets initiaux la conique et le point M. Note technique : la macro proposée ici est appliquable directement aux 2°, 3° et 4° points constituants de la conique, ce qui servira dans les constructions suivantes. On remarquera que pour un cercle, le point de Frégier est un invariant, c'est son centre. Pour une ellipse, le point de Frégier est ainsi, d'une certaine façon, une généralisation du centre du cercle comme point commun des cordes vues d'un point sous un angle droit.

Lieu du point de Frégier

 Le lieu du point de Frégier pour une conique à centreest une conique homothétique dans une homothétie de centre le centre de la conique (sauf hyperbole équilatère abordée plus loin).

Sur la figure ci-contre, on propose une vérification expérimentale de cette propriété : à partir de FB le point de Frégier de B, on construit le point K, une des intersections de la conique et de la droite (OFB) et l'homothétique de deux autres points constituants de la conique dans l'homothétie de centre O transformant K en FB. On construit enfin les symétriques de ces deux points par rapport à O. On peut alors tracer la conique passant par ces 5 points. Le lieu du point de Frégier FM d'un point M de la conique de base décrit effectivement cette seconde conique. LFregEH.fig

Cas de la parabole   Le lieu du point de Frégier d'une parabole est une parabole translatée. Dans la figure précédente la parabole est construite comme transformée par une homologie harmonique.   LFregP.fig

Normale à une conique

Développée d'ellipse en taille réelle (21 K)

Par définition même du point de Frégier (comme homologue harmonique du centre d'un cercle ...) il est clair que le point de Frégier F d'un point A est sur la normale de la conique en A. Ainsi, la droite (AF) est normale à la conique, ce qui permet de transformer la figure précédente en une macro Normale à une conique. Il est clair que c'était possible dès que l'on savait construire une tangente, par les rayons conjugués. On peut en profiter pour revisiter les développées des coniques, comme enveloppe des normales : (les réduction d'écran sont un peu agressives à l'oeil, on pourra les charger en taille réelle)

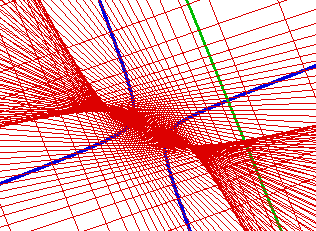
Développée d'hyperbole en taille réelle (24 K)

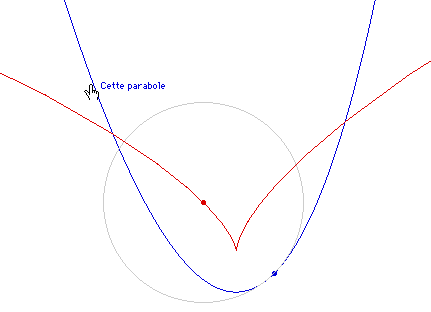
Développée de parabole en taille réelle (17 K)

Avec le point de Frégier, nous allons construire au prochain paragraphe directement le centre de courbure associé à un point, ce qui va permettre de tracer la développée d'une conique comme lieu de point, au lieu de l'obtenir par enveloppe de droite.

Cas de l'hyperbole équilatère

Il y a là un cas particulier puisque, d'un point d'une hyperbole équilatère, on ne voit pas de corde - à distance finie - sous un angle droit. Ces cordes sont rejettées à l'infini, et le point de Frégier aussi, dans la direction de la normale.

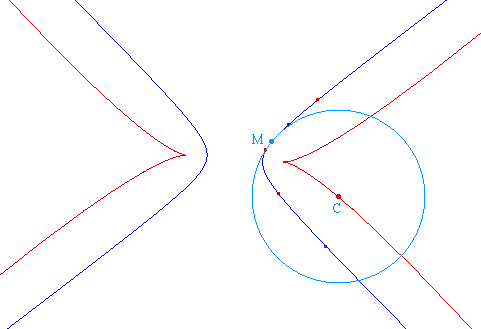
Il est remarquable que Cabri - là encore - résiste trés bien au passage à l'infini : une macro de normale à une conique, construite à partir du point de Frégier s'applique sans problème à une hyperbole équilatère. NormHEq.fig On peut aussi préférer faire l'expérience soi même et dans ce cas : Charger les macros Hyperbole équilatère et Normale à une conique Note : la macro Hyperbole équilatère construit l'hyperbole à partir de son centre, une asymptote et un point de l'hyperbole. Ce choix peut surprendre mais il a l'avantage que ce point se comporte comme un effet zoom, selon qu'on le place près ou loin des asymptotes. Sinon, pour construire une hyperbole équilatère passant par 4 points, il suffit de construire l'orthocentre d'un des triangles formé par ces 4 points, et de tracer la conique passant par ces 5 points. En effet, par 4 points orthocentriques il ne passe que des hyperboles équilatères.

Centre de courbure - Cercle osculateur

Si on souhaite faire soi-même la construction proposée dans ce paragraphe, on aura besoin de charger les trois macros suivantes :

Homologie (d'une conique) Point de Frégier et Polaire d'un point.

Théorème (de Frégier) utilisé : Soit A un point d'une conique. La transformée de cette conique dans une homologie de centre A est un cercle si et seulement si la droite "delta" (homothétique de l'axe dans h_A,1/2) est la polaire du point de Frégier associé à A, par rapport à la conique.

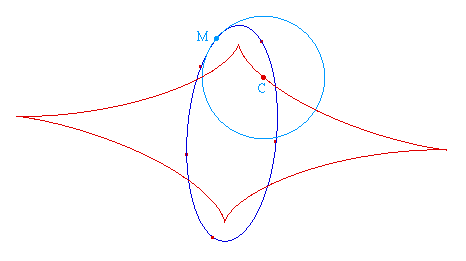
À partir d'un point sur objet A d'une conique, on construit son point de Frégier F, puis la polaire de F par rapport à la conique. L'axe (d) de l'homologie est l'homothétique de la polaire dans l'homothétie de centre A et de rapport 2. L'homologue de la conique par cette homologie est alors une ellipse circulaire (reconnue comme telle par Cabri), donc un cercle, tangent à la conique en A. La droite parallèle à (d) passant par A étant globalement invariante, on en déduit que le cercle symétrique du cercle image dans la symétrie de centre A coupe la conique de départ en un unique point B : l'intersection de la conique et de la droite. Cela signifie que le contact en A entre la conique et ce cercle est d'ordre 3 : nous venons de tracer le cercle osculateur à la conique en A, son centre C étant le centre de courbure de la conique en A. Le point C est directement construit comme intersection de (AF) et de la médiatrice de [AB]. La figure Osculat.fig, ou La macro Osculat.mac.

Tracé des développées par lieu de points

Il suffit d'utiliser la macro précédente, c'est le lieu du centre de courbure :

Menu général