

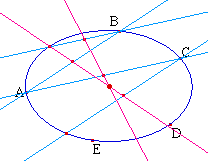
Le centre d'une conique se trouve
sur le lieu des milieux de cordes parallèles. Il
suffit de prendre deux tels lieux : à partir de trois
points A, B, C, de la conique (parmi les 5 points
constituants) on construit C' intersection de la conique et
de la parallélèe à (AB) passant par C
et B' la parallèle à (AC) passant par B. Le
lieu des milieux des cordes parallèles à (AB)
est la droite passant par les milieux de [AB] et
[CC'], de même le lieu des milieux des cordes
parallèles à (AC) est la droite passant par
les milieux de [AC] et de [BB']. Le centre
de la conique est à l'intersection.
![]() La figure CentreC.fig.
La figure CentreC.fig.![]() La macro Centre
d'une conique.
La macro Centre
d'une conique.
 |
 |
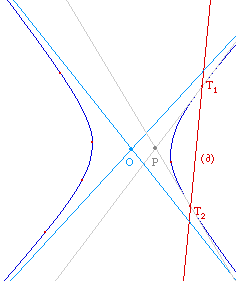
Cabri est particulièrement
stable en ce qui concerne le passage à l'infini. On
peut s'en servir pour transformer des tangentes en
asymptotes. Soit une hyperbole dont on a construit le centre
O. On construit la polaire d'un point P extérieur
à l'hyperbole, puis les tangentes issues de P, dont
les points de contact sont les intersections de l'hyperbole
et de la polaire.
Il suffit alors
de redéfinir le point P
comme identifié à O
pour que les points de contacts
soient renvoyés à l'infini : les tangentes se
transforment naturellement en asymptotes.
![]() La
macro Asympt.mac
La
macro Asympt.mac
Note technique :
On remarquera que sur ces
droites, construites sur la base de points à
l'infini, on ne peut pas poser de points sur objet. En fait
ces points sur objet sont construits à l'infini, on
peut ainsi mesurer l'angle entre les asymptotes. Il reste
que l'on peut prendre l'intersection de ces asymptotes avec
d'autres objets, ce qui est l'essentiel.
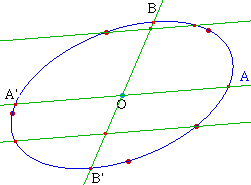
Le milieu des cordes
parallèles à un diamètre d'une conique
est la direction du diamètre
conjugué.
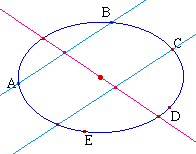
Il suffit de tracer, à
parti des points constituants de l'ellipse, deux cordes
parallèles à un rayon [OA]. Le rayon
conjugué est porté par la droite passant par
le milieu de ces cordes. Pour l'ellipse, le diamètre
conjugé est fourni par l'intersection avec la
conique.
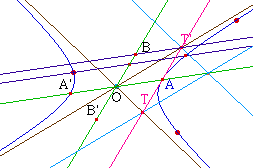
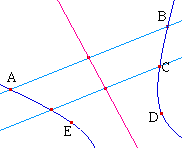
Dans le cas de l'hyperbole la
droite portant le rayon conjugué ne coupe pas
l'hyperbole. La longueur d'un rayon conjugué se
construit alors en utilisant les asymptotes. Soit
[AA'] un diamètre dont on cherche le
diamètre conjugué. La tangente à
l'hyperbole en A coupe l'asymptote en T et T'. Soient B et
B' telque OATB et OAT'B' soient des parallèlogrammes,
alors le conjugué de [AA'] est
[BB'].
Note
: la construction de (TT') est
aisée car une des propriétés de la
tangente est que A est milieu de [TT'].
![]() DiaConj.fig.(la
figure contient les deux cas)
DiaConj.fig.(la
figure contient les deux cas)
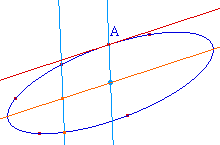
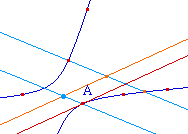
D'aprés le rappel
précédent, il est clair que la tangente en un
point A a pour direction le diamètre conjugué
du rayon [OA]. La seule connaissance de la direction
du diamètre conjugué suffit. Comme on dispose
déjà du centre, une seule autre corde est
à tracer.
![]() La macro Tangente
en un point (fichier
TgtePtCn.mac).
La macro Tangente
en un point (fichier
TgtePtCn.mac).
Note technique
: la macro proposée est
construite de telle manière qu'elle s'applique
également à 4 des 5 points constituants de la
conique (on ne peut prendre la tangente en le second point
constituant).
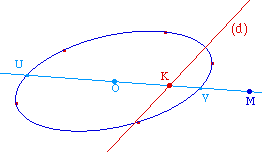
Observation :
Quand M parcourt la droite, sa
polaire est parallèle à une direction fixe qui
n'est autre que celle du diamètre conjugué de
la droite prise au départ (penser à la
tangente par exemple quand M est sur la
conique).
![]() ExpPol.fig
ExpPol.figOn notera aussi que, si on note U
et V les intersections du diamètre initial avec la
conique, et K l'intersection de cette droite avec la
polaire, par définition de la polaire,
les couples (U, V) et (M, K)
sont conjugués
harmoniques.
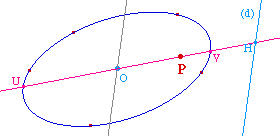
Construction du pôle
:
D'après ce qui
précède, il est clair que le pôle est
sur la direction conjuguée à celle de la
droite. On trace donc le diamètre parallèle
à la droite de base, on construit sa direction
conjuguée.
Cette droite coupe la conique en U
et V, et la droite dont on cherche le pôle en H. Il
suffit de faire une division harmonique pour trouver le
pôle P entre (U, V) et (H, P).
![]() La figure PoleDrt.fig
ou La macro PoleDrt.mac
La figure PoleDrt.fig
ou La macro PoleDrt.mac