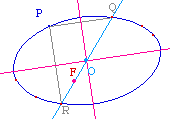
 |
Pour déterminer les axes d'une conique - dont on a construit le centre O par une macro précédente - il suffit de pouvoir construire un triangle rectangle inscrit dans la conique.Pour faire la figure ci-contre, on a besoin de :
|
|
|
Pour cela, on prend un point P de la conique. Soit F le point de Frégier associé (la macro précédente s'applique directement à trois des points constituants). La droite (CF) coupe la conique en deux points P et Q qui conviennent. Les médiatrices de [PQ] et de [PR] sont les axes de la conique.
|
 |
|
|
|
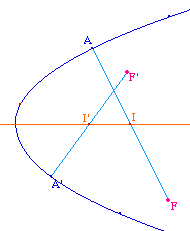
Soit O le centre de l'ellipse, et F le point de Frégier d'un point M de l'ellipse de centre O. Alors l'axe focal est la bissectrice intérieure de l'angle MOF.Comme on sait que la macro Frégier peut s'appliquer à trois des points constituants de l'ellipse, on peut faire une figure transformable en macro sans adjonction de point supplémentaire.
|
|
|
En fait la construction est encore valable pour les hyperbole à excentricité strictement inférieure à sqrt(2) - ie jusqu'à l'hyperbole équilatère non comprise - comme illustré à gauche, et ensuite, pour une excentricité supérieure à sqrt(2), l'axe focal est la bissectrice extérieure du même angle :Sur l'illustration de droite, on voit que la même construction donne l'autre axe.Il faut donc une construction spécifique pour l'hyperbole. |
 |
Charger les macros Asymptote
à une hyperbole (fichier
Asympt.mac)
et Polaire d'un point
(fichier
Polaire.mac)
|
|
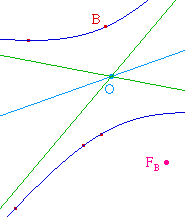
Pour traiter les deux cas de l'hyperbole, on peut utiliser un résultat déjà mentionné sur la polaire d'un point (en Page 1). On a vu en effet que si un point P est à l'extérieur de l'hyperbole mais entre l'hyperbole et ses asymptotes, la polaire de ce point coupe l'hyperbole en deux points d'une même branche.On est alors assuré que cette droite coupe les asymptotes en deux points U et V tels que l'axe focal est la bissectrice intérieure de l'angle UOV, où O est le centre de l'hyperbole.
|
Menu général
