Université d'été 96

Extraits de la conférence de Michel Guillerault

6 - Construction des foyers d'une Cabri-conique

Préambule d'abraCAdaBRI

 

Dans sa conférence, Michel Guillerault a proposé trois constructions des foyers d'une conique à centre. Ces constructions utilisent toutes une référence à l'axe focal. Comme, au moment de la rédaction de ces pages (11/96) nous ne disposons pas d'une construction Cabri simple qui donne l'axe focal pour tous les cas d'ellipse et d'hyperbole, nous allons être amené à réaliser la même construction sur deux cas différents de figure. La situation sera, à chaque fois, améliorée en une macro qui donnera bien les foyers pour une conique dans tous les cas de figure, mais cela restera non totalement satisfaisant dans la mesure où les foyers seront deux couples de points différents dans les deux cas. Cela signifie que si on devait faire une construction à partir d'eux, il faudrait appliquer cette construction deux fois.

Cette page, qui reflète l'état de l'art (Cabri) sur le thème des foyers d'une conique en juillet 96 illustre bien pour nous toute l'ambiguité que peut contenir la notion de plan de construction dans l'environnement "papier/crayon". Quand un texte propose "on considère l'axe focal", parle-t-il encore en termes algorithmiques, ou, en invitant son lecteur à opérer un choix, rentre-t-il dans un domaine perceptif ? La difficulté rencontrée ici de Cabri-construire l'axe focal d'une conique dans tous les cas, focalise (...) notre attention sur cette question ...

Construction utilisant les tangentes aux sommets

Pour réaliser cette figure en direct, il est utile de :

Charger les macros Axe focal d'une ellipse (fichier AxeFocE.mac) et/ou Axe focal d'une hyperbole (fichier AxeFocH.mac) mais aussi de la macro Tangente en un point d'une conique (fichier TgtePtCn.mac)

On mène les deux tangentes (d) et (d') aux sommets de la conique sur l'axe focal. Une tangente en un point M de la conique coupe ces deux tangentes en deux points K et K'. Alors le cercle de diamètre [KK'] coupe l'axe focal aux deux foyers de la conique.

Rappel : la macro Tangente est appliquable directement à 4 des 5 points constituants de la conique, le point M peut être un de ceux là.

Transformation de la figure en macro

Pour réaliser cette figure en direct, il est utile de :

Charger la macro Axes d'une conique (fichier AxesHE.mac)et éventuellement Asymptotes d'une hyperbole (fichier Asympt.mac)

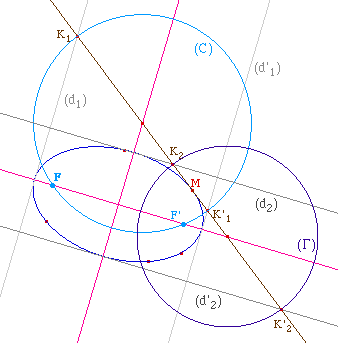
On refait la figure, sur la base d'une ellipse, avec les deux axes - ci contre les objets sont indicés 1 sur l'axe focal et 2 sur l'axe non focal. On remarquera que pour une ellipse, il n'y a toujours que le cercle construits à partir de l'axe focal qui coupe effectivement l'axe, l'autre cercle ne coupe jamais l'axe à partir duquel il est construit. FoyE1Mac.fig (qui contient aussi les constructions ci-dessous avec les asymptotes) On a déjà vu (à la page précédente) que la construction de l'axe focal d'une hyperbole est la même que celle d'une ellipse si l'hyperbole est d'excentricité strictement inférieure à sqrt(2) - angle inférieur à 90° - et elle est différente (changement de l'axe) avec une excentricité supérieur à sqrt(2) - angle supérieur à 90°. 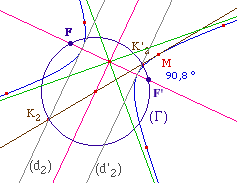Sur les illustrations ci-dessous on observe que c'est bien le cercle (C) - à gauche - qui aboutit aux foyers dans le premier cas (ellipse) et le cercle "Gamma" dans le second cas, à droite (on a déplacé seulement un point constituant de la conique d'un pixel d'un dessin à l'autre).

Rappel technique : même si on ne peut pas prendre de points sur objet des asymptotes à distance finie, cela n'empèche pas de mesurer l'angle entre les deux droites, en utilisant justement que ces points sur objet existent, mais sont rejetés à l'infini.

Pour la transformation en macro, on a choisi de colorer les foyers différemment pour bien mettre en évidence que si l'on construit une macro qui renvoie les deux couples de points F et F' dans les deux cas ci-dessus, l'utilisateur aura une macro qui renvoie bien les foyers d'une conique dans tous les cas, mais obtenus à partir de deux paires de points différents.

Charger la macro Foyers d'une conique (fichier Foyers1.mac)

Construction utilisant l'axe non focal

Nous irons un peu plus vite en voyant directement la macro de la seconde méthode, très proche de la première.

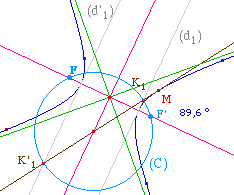
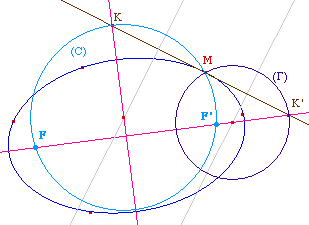
	Cette fois on note K l'intersection de la tangente en M avec l'axe non focal. La médiatrice de [KM] coupe cet axe en un point. Le cercle centré en ce point et passant par M coupe l'axe focal aux foyers. Autre présentation possible : en prenant M' le symétrique de M par rapport à l'axe non focal, les tangentes à la conique en M et M' se coupent en K. Le cercle construit est alors présenté comme le cercle circonscrit à M, M', K. Sur l'illustration ci contre, on a aussi réalisé la même construction pour l'autre axe. Comme dans le cas précédent, ce second cercle, pour l'ellipse, ne coupe jamais l'axe à partir duquel il est construit. Foy2Mac.fig (qui contient aussi les constructions ci-dessous avec les asymptotes)
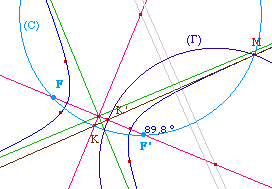
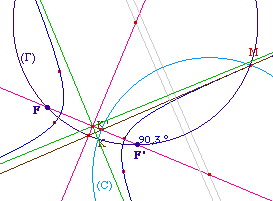
Le comportement pour l'hyperbole est le même que dans la méthode précédente. Voici une illustration de chaque cas qui reprent les même notation (et les mêmes couleurs d'illustration).

On pourrait faire, avec cette seconde méthode, une macro qui se comporterait de la même façon que la précédente, et qui donc ne présente pas d'avantage particulier.

Utilisation du centre de courbure

si vous souhaitez réaliser la figure suivante, vous aurez besoin (en plus de la macro Axes) de :

Charger la macro Centre de courbure (on effacera le cercle osculateur, inutile dans la suite)

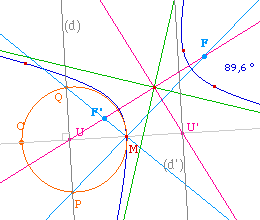
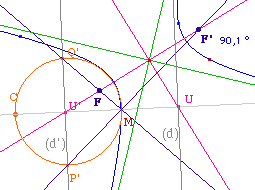
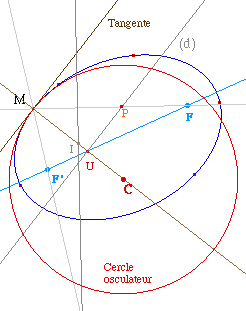
	À partir d'un point M de la conique - l'un des points constituant peut convenir - on construit son centre de courbure C. La droite (MC) coupe l'axe focal en U. Soit (d) la perpendiculaire à (MC) en U, et P et Q les intersection de cette droite avec le cercle de diamètre [MC]. Alors les droites (MP) et (MQ) coupent l'axe focal aux foyers de la conique. Rappel : la macro Frégier étant appliquable directement à 3 des 5 points constituants de la conique, il en est de même du centre de courbure. On peut préférer utiliser un point sur objet M pour observer que les points F et F' sont bien invariants quand M se déplace sur la conique. Lancer une telle figure FoyerOsE.fig
Transformation de la figure en macro Comme dans les deux méthodes précédente, on fait la même chose avec l'autre axe. Dans les figures ci-dessous, on a "primé" les noms des objets équivalents pour l'autre axe - et mis les couleurs correspondantes des méthodes précédentes. Sur la première illustration, la branche de construction associée à la droite (d') est sans effet, puisque le cercle ne la coupe pas. Mais en déplaçant un point constituant d'un pixel, l'hyperbole bascule de l'autre côté de l'hyperbole équilatère et c'est la branche de la droite (d) qui est devient sans effet : On retrouve le même comportement que dans les méthodes précédentes, puisque toutes ces méthodes sont des variantes de l'utilisantion de l'axe focal.
FoyOsMac.fig

Construction du cercle osculateur

Pour réaliser la figure suivante, on utilisera la macro Foyer d'une conique réalisée, et disponible, plus haut et La macro Tangente à une conique (fichier TgtePtCn.mac) La figure précédente est plus souvent utilisée pour, au contraire, construire le centre de rayon de courbure à partir des foyers : Soit M un point sur objet d'une conique dont on connait les foyers F et F'. On trace la normale en M à la conique par la perpendiculaire à la tangente (construite à partir des diamètes conjugués). Cette normale coupe la droite (FF') en U. La perpendiculaire à cette droite coupe (MF) en P. La médiatrice de [MP] coupe la normale en M un point I. D'après ce qui précède le cercle de centre I passant par M contient le centre de courbure, ou encore, le centre de courbure C est les symétrique de M par rapport à I. C'est la méthode classique d'obtention du centre de courbure. FoyVerOs.fig

Foyer d'une parabole

Le foyer d'une parabole est beaucoup plus facile à construire, puisque l'on ne traite qu'un seul cas de conique. La première méthode vue ci-dessus revient, pour la parabole, à utiliser le fait que le projeté orthogonal du foyer sur une tangente est aussi sur la tangente au sommet :

Pour faire la figure en direct, il est plus facile de :

Lancer une figure Parabole par homologie harmonique et charger les macros Axe d'une parabole , Tangente à une parabole

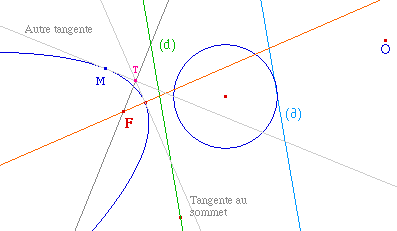
La parabole est construite à partir de l'homologie harmonique d'un cercle dans laquelle la droite "delta" est tangente au cercle. Les paramètres de l'homologie - son centre O et son axe (d) - permettent de modifier la figure. Avec l'axe de la parabole, on construit la tangente au sommet. Une autre tangente à la parabole (construite par exemple à partir d'un point M constituant de la parabole pour une transformation en macro) coupe la première en un point T qui est la projection orthogonale du Foyer sur cette seconde tangente. D'où la construction du foyer, puisque l'on sait qu'il est sur l'axe. FoyerP1.fig

Autre méthode

On peut essayer de ne pas utiliser l'axe focal et la tangente au sommet. Par exemple, c'est une autre façon d'exprimer la propriété précédente, on sait que le symétrique du foyer par rapport à une tangente est sur la directrice. D'où les symétriques du foyer par rapport à 3 tangentes sont alignés, c'est-à-dire (droite de Steiner d'un triangle) le foyer est sur le cercle circonscrit au triangle formé par l'intersection de trois tangentes. Pour faire la figure suivante, on peut : Charger une macro Cercle circonscrit 3 points Trois premières tangentes forment un triangle PQR. Le foyer est sur son cercle circonscrit. On construit une quatrième tangente, et un triangle (par exemple SQT. Le foyer est alors à l'intersection du cercle circonscrit à SQT et du précédent cercle. FoyerP2.fig

Macros Foyers et directrices

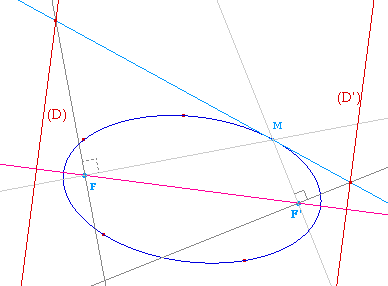
Une fois que l'on dispose des foyers, il est immédiat de constuire les directrices, par exemple à partir d'une tangente dans le cas d'une conique à centre. On utilise simplement que, si on note T l'intersection de la tangente en M avec la directrice associée au foyer F, le triangle MFT est rectangle en F, ce qui permet de construire T sur la tangente donc la directrice. Compte tenu de ce que l'on a dit sur la macro 'Foyers", il faut faire deux fois la construction, et, comme pour les foyers, les directrices, ne sont pas les mêmes droites dans tous les cas de figures. La figure FoyDir.fig ou la macro Foyers et directrices (fichier FoyDir.mac) pour une hperbole ou une ellipse.

Menu général