Rappel des notations

 

Théorème de Carnot Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets. Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi :

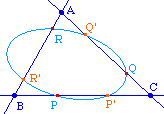
Notation utilisée pour des preuves barycentriques : on se place dans le repère affine (A, B, C). Posons P (0, 1, -p), P' (0, -p', 1) ce qui signifie que
De même, on pose Q (-q, 0, 1) et Q' (1, 0, -q') puis R (1, -r, 0) et R'(-r', 1, 0), ce qui induit des relations analogues entre les coordonnées barycentriques et les rapports de mesures algébriques.

Avec ces notations, le théorème de Carnot s'écrit : les 6 points sont sur une conique ssi

Autour des paraboles

On sait que par 4 points passent en général deux paraboles. A quelles conditions sur R et R' l'une des deux parabole passant par P, P', Q et Q' passe-t-elle aussi par R et R' ? Cas particulier de deux points de contact (P = P' et Q = Q') : on sait que cette condition définit entièrement la parabole, conditions sur r et r' pour que les 6 points soient sur une parabole. Constructions Cabri.

Cas des céviennens concourantes ou parallèles

On sait, à partir de 5 points d'une conique à centre construire son centre. Relations entre le centre de la conique et les deux points de concours M et N. Cas particulier des coniques tritangentes et d'un seul centre cévien L : à quelles conditions le centre de la conique et le centre cévien sont-ils confondus; y-a-t-il d'autres cas que le centre de gravité du triangle ? Cet exercice peut être l'occasion de reprendre ce thème des céviennes par un calcul barycentrique à partir des coordonnées barycentriques de M et N.

Dans le cas où l'un des triplet de céviennes sont parallèles - ou les deux - peut-on préciser, en fonction du point mobile (P et P' dans la page consacrée à ce cas particulier), la nature de la conique obtenue ?

Cas des points symétriques

On a vu l'exemple des coniques passant par les six points de contact des cercles exinscrits au triangle, ou encore des cercles cercles exinscrits et du cercle inscrit. Caractérisations euclidiennes de ces deux coniques. 

Menu général