Notations du théorème de Carnot

Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets.

Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi :

Le cercle inscrit à un triangle est une conique tritangente au triangle, donc les droites (AP), (BQ) et (CR) sont parallèles ou concourantes. Elles ne peuvent pas être parallèles par des arguments angulaires (par exemple), elles sont donc concourantes en un point dit :

Point de Gergonne

Utiliz02.fig

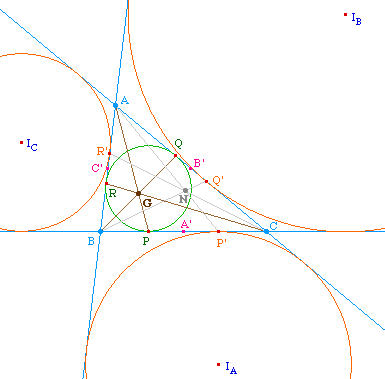Puisque le cercle exinscrit associé à l'angle A - de centre IA - est tangent à (BC) en P' symétrique de P par rapport au milieu A' de [BC], les droites ainsi construites (AP'), (BQ') et (CR') sont concourantes comme isotomiques des droites (AP), (BQ) et (CR). En particulier elles sont concourantes en un point N, isotomique du point de Gergonne, appelé :

Point de Nagel.

Utiliz03.fig

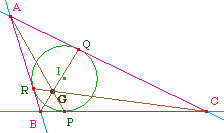
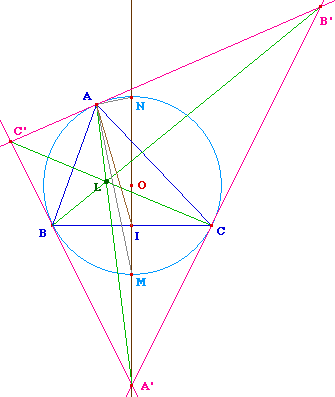
On construit le triangle A'B'C' pour lequel le cercle circonscrit à ABC est son cercle inscrit, tangent en A, B et C.

Le point de Gergonne du triangle A'B'C' est appelé point de Lemoine du triangle ABC.

Théorème : le point de Lemoine est l'isogonal du centre de gravité par rapport au triangle ABC.

Preuve succinte (sera plus détaillée dans le dossier "angle et cocyclicité" quand il sera rédigé).

Il faut montrer que la médiane (AI) et la droite (AA') sont isogonales par rapport à (AB) et (AC).

Cela peut se faire par les lignes de niveau et produit scalaire. On montre par exemple - produit scalaire - que (en mesure algégrique) OA'/OM = OM/OI et alors, par somme et différence, on arrive (toujours en mesures algébriques) à

NA'/NI = - MA'/MI = k

I et A' étant donnés, la ligne de niveau XA'/XI = k est le cercle de diamètre [MN] et donc AM est bissectrice intérieure et (AN) extérieure à AIA', ce qui assure le résuultat si on sait déjà par ailleurs que dans cette configuration (AM) est bissectrice intérieure de ABC (c'est le point P1 de la page II.4 sur l'exemple du cas des points symétriques.