Cercles inscrit et exinscrits

Propriétés et notations générales

[1 - Définitions des bissectrices] [2 - Pieds des bissectrices] [3 - Propriètés des points de contacts]
[4 - Diverses relations métriques] [5 - Théorème de Feuerbach]

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

 

L'existence du cercle inscrit et des cercles exinscrits est une conséquence immédiate de la propriétés des bissectrices d'être l'ensemble des points à meême distance de deux droites ...

 

BisInt3P.mac (objets initiaux les 3 points, objets finaux les 3 bissectrices)

CInsc3P.mac (objets initiaux les 3 points, objet final le cercle inscrit)

CInscTR.mac (objet initial le triangle, objet final le cercle inscrit)

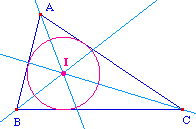
CInsExO1.fig (figure ci-contre)

BissEX3P.mac

(objets initiaux les 3 points, objets finaux les 3 bissectrices extérieures)

CExins3P.mac

(objets initiaux les 3 points, objets finaux les 3 cercles exinscrits)

CExinsTR.mac

(objet initial le triangle, objets finaux les 3 cercles exinscrits )

 

Coordonnées barycentriques

En notant a = BC, b = AC et c = AB, on a :

A

B

C

I

a

b

c

IA

-a

b

c

IB

a

-b

c

IC

a

b

-c
  

... ce qui est aussi vrai en géométrie hyperbolique, mais aussi que deux bissectrices extérieures et une intérieure associées sont concourantes, ce qui n'est pas toujours le cas dans cette géométrie : les cercles exinscrits hyperboliques n'existent que si les bissectrices sont concourantes. Le cercle inscrit hyperbolique existe toujours.

 

Sources documentaires pour ces pages :

"La géométrie du triangle" - Y. & R. Sortais - Edition Hermann  

Les ouvrages des Editions Gabay (Lebossé & Hermery - Delteil & Caire)

 

 

[1 - Définitions des bissectrices] [2 - Pieds des bissectrices] [3 - Propriètés des points de contacts]
[4 - Diverses relations métriques] [5 - Théorème de Feuerbach]

 

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

 

Menu général