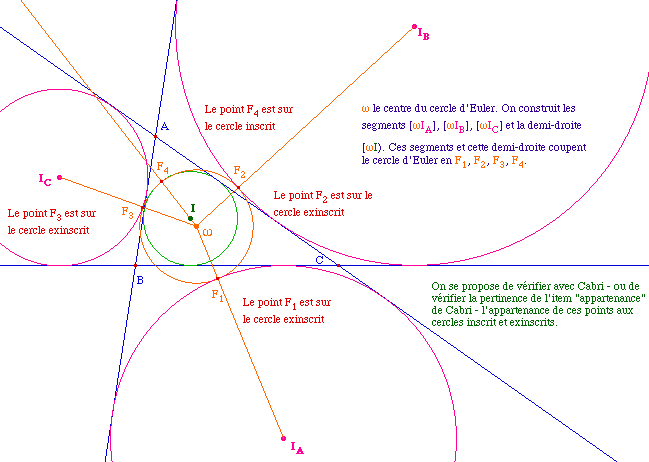
5 - Le Théorème de Feuerbach
[Présentation
générale] [1 -
Définitions des bissectrices] [2
- Pieds des bissectrices]
[3 - Propriètés des points de
contacts] [4 - Diverses relations
métriques]
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]
Resultat et Cabri-test | Principe de preuve | Preuve

Resultat et Cabri-test | Principe de preuve | Preuve
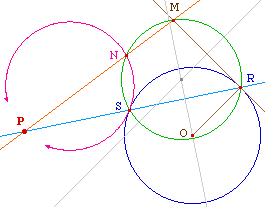 |
1. Un lieuOn considère un cercle de centre O et P un point extérieur au cercle. Soit R un point du cercle et d la tangente au cercle en R.À tout point M de d on associe le point N tel que (en mesure algébrique) PM.PN soit la puissance de P par rapport au cercle.Alors le lieu de N est un cercle passant par P tangent au cercle initial en l'autre point de (PR) du cercle, privé de P.Preuve par cocyclicité ci-dessous Remarque : pour la construction, il est clair que l'on construit N comme l'inverse de M dans l'inversion de centre P qui transforme R en S (d'où le cercle vert ci-contre). L'image de la tangente au cercle est alors un cercle tangent au cercle initial passant par le centre de l'inversion. |
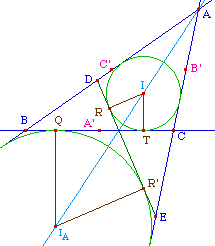 |
2. Le cercle d'Euler comme lieu précédent
|
Resultat et Cabri-test | Principe de preuve | Preuve

|
|
2.a. Le milieu K de [CD] est à l'intersection de (AI) et (A'B').Tout d'abord K est sur la médiatrice de [CD], comme ACD est isocèle en A, cette médiatrice est la bissectrice (AI). Donc K est sur (AI). Par ailleurs, dans BCD, le théorème des milieux abouti à ce que K soit aussi sur (A'B').2.b. A'K = A'T = A'Q.En effet A'K = BD/2 et BD = AT. Un calcul classique de CT en fonction des côtés du triangle aboutit (pour AB>AC) à A'K=A'T = (AB-AC)/2.2.c. En mesure algébrique (ema) A'M.A'B' = A'K2 = A'L.A'C'.Thalès dans JAB donne
(ema) A'M/A'K = BD/BA.
|
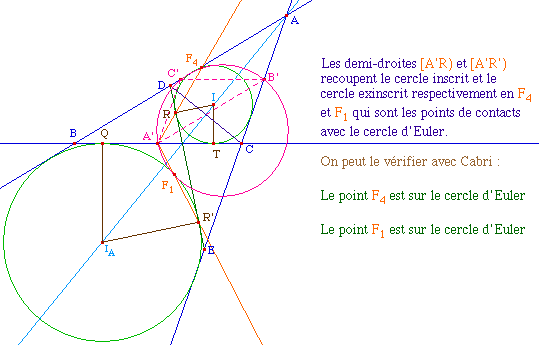
Bien-sûr une preuve par inversion serait plus adaptée ...
Resultat et Cabri-test | Principe de preuve | Preuve
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]