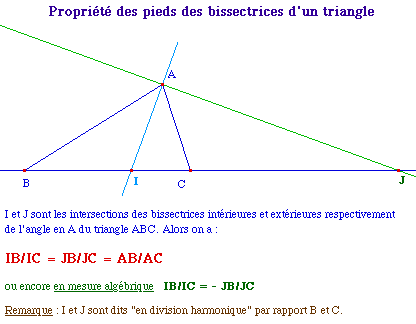
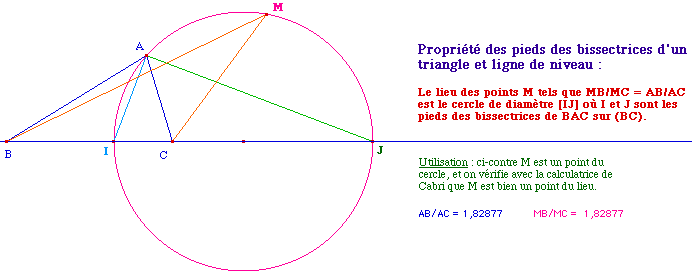
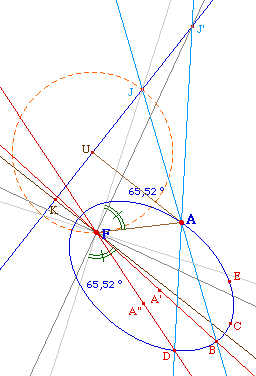
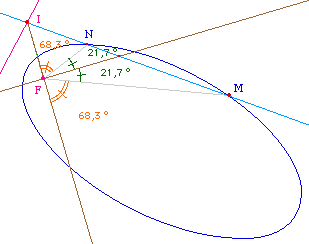
2 - Pieds des bissectrices
[Présentation
générale] [1 -
Définitions des bissectrices] [3
- Propriètés des points de contacts]
[4 - Diverses relations
métriques] [5 -
Théorème de Feuerbach]
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]