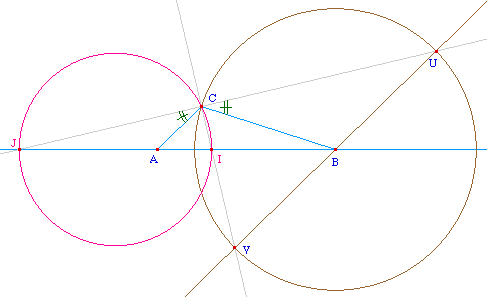

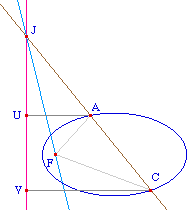
J est un point de la directrice.
La droite (JA) recoupe la conique en C.
L'excentricité de la conique s'écrit
:
![]()
Il en résulte donc les
égalité :
![]()
C'est-à-dire que (FJ) est
bissectrice de l'angle AFC. Ce résultat
(c'est le
thèorème de
Poncelet) permet de construire
l'intersection de la conique et de la droite (JA) : c'est le
point C de la droite pour lequel (FJ) est bissectrice de
l'angle AFC.
Remarque :
On observera à
l'occasion que la bissectrice n'est intérieure que
dans le cas où les deux points A et C sont sur deux
branches différentes de la conique.
Une première utilisation du
théorème.
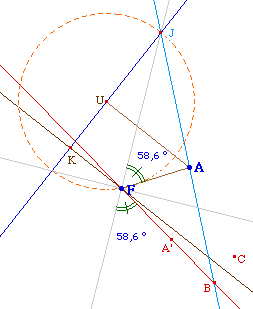
K et U sont les projections
orthogonales de F et A sur la directrice. Le cercle de
centre U passant par F recoupe la directrice en J. Si A est
sur l'axe focal (FK), F, J, A ne sont donc pas
alignés. Si A n'est pas sur l'axe focal, UF est
rationnellement incommensurable avec les coordonnées
de A et donc F, J, A ne peuvent être
alignés.
Soit alors A' le symétrique
de A par rapport à la droite perpendiculaire à
(JF) en F. La droite (FA') coupe la droite (JA) au point B
cherché. On obtient un troisième point de la
conique en construisant C le symétrique de B par
rapport à l'axe focal.
![]() Lancer la figure
PonceInt.fig
partielle.
Lancer la figure
PonceInt.fig
partielle.On observera par exemple que (FJ)
peut aussi être bissectrice
intérieure.
En plaçant la directrice
verticale à l'écran, on vérifiera que
si l'on peut positionner à l'écran les points
F, J, A quasiment alignés, par construction ils ne le
sont pas pour Cabri : les points B et C existent dans tous
les cas de figure.
Une seconde utilisation du
résultat.
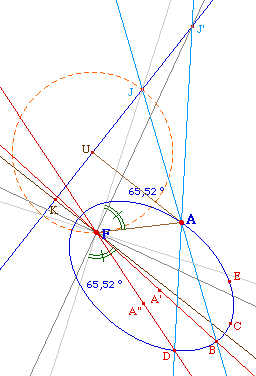
On a choisit de prendre comme
second point de la directrice le point J' symétrique
de U par rapport à J. On construit A" comme A'. On
obtient un point D, et son symétrique E fait le
cinquième point de la conique.
![]() Lancer la figure
CnkDFA2.fig
finale.
Lancer la figure
CnkDFA2.fig
finale.
![]() Charger la macro
Conique par Dir.
Foyer 1 pt correspondante (fichier
CnkDFA2.mac)
d'objets initiaux la directrice, le foyer F et le point A
.
Charger la macro
Conique par Dir.
Foyer 1 pt correspondante (fichier
CnkDFA2.mac)
d'objets initiaux la directrice, le foyer F et le point A
.
Le comportement sur les paraboles
|
À partir d'une droite D et d'un point A, construire le cercle de centre A et tangent à la droite. Soit F un point sur objet de ce cercle. Appliquer la macro à D, F, A. On obtient une parabole.Redéfinir alors F comme point de base. En déplaçant le point, la conique devient une ellipse ou une hyperbole.Redéfinir à nouveau F comme point sur objet du cercle, la conique redevient une parabole. |
Pour le plaisir : avec des hyperboles équilatères
|
Il ne s'agit pas de tester la robustesse de la macro, mais juste d'illustrer la qualité de Cabri II. Le cercle de centre H passant par A coupe la droite - destinée à devenir directrice - en I.Un point F du cercle de centre A passant par I est le foyer d'une conique de directrice D passant par A qui est toujours une hyperbole équilatère, de par son excentricité (racine carrée de 2).Cabri II le reconnaît...
|