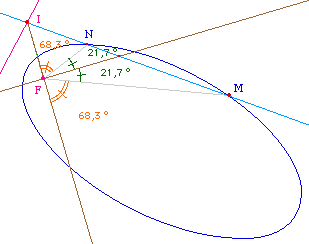
La conique est construite avec la
macro indiquée plus haut, le point A est
caché. I est un point de la directrice, M de la
conique. (IM) recoupe la conique en N. On a tracé le
segment [IF] et la perpendiculaire à ce
segment en F. Le théorème de Poncelet dit que
la droite (IF) et sa perpendiculaire sont les bissectrices
extérieures et intérieurs (non respectivement,
cela dépend de la conique) de l'angle
MFN.
Quand M décrit la conique,
(IF) et sa perpendiculaire sont fixes, elles restent
bissectrices des angles.
Rappel (d'une page
précédente) : On
observera que la bissectrice (IF) n'est intérieure
que dans le cas où les deux points A et C sont sur
deux branches différentes de la conique.
![]() TgtPonc1.fig.
TgtPonc1.fig.
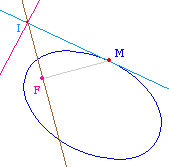
Il est clair que quand M est
confondu avec N, par principe de continuité, le
triangle applati a toujours la droite (IF) comme
"bissectrice" de MFN. Cela signifie que :
Soit une conique de directrice D,
de foyer F, et M un de ses points (autre que les sommets).
La tangente en M à la conique coupe la directrice en
un point I tel que le triangle IFM soit rectangle en
F.
On dit aussi que le segment de la
tangente soustendu par la directrice est vu du foyer sous un
angle droit.
![]() La
macro Tangente
en un point d'une conique par D F
M d'objets initiaux la directrice,
le foyer et le point d'où l'on veut la tangente
(fichier
TgCnkDF1.mac).
La
macro Tangente
en un point d'une conique par D F
M d'objets initiaux la directrice,
le foyer et le point d'où l'on veut la tangente
(fichier
TgCnkDF1.mac).

|
|
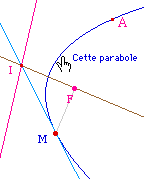 |

Puisqu'une conique est
définie par une directrice, son foyer associé
et un point, ce point peut être construit, par la
proprité de l'angle droit au foyer quand on
connaît une tangente. Donc une conique est
entièrement déterminée par une
directrice, le foyer associé et une tangente, comme
sur la figure ci-contre.
Toutefois cette tangente peut
être parallèle à la directrice, et on
peut être amené à construire une conique
spécifiquement dans ce cas.
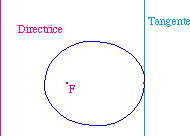
Il faut alors faire intervenir une
macro
logique qui rend compte si deux
droites sont ou non parallèles. Dans la rubrique
Alice,
au chapitre des Incidences,
un telle macro a déjà été
construite. On peut la charger (Parall.mac)
pour terminer soi-même la figure : cette macro renvoie
sur un point d'une des deux droites un point qui n'existe
que si ces droites sont parallèles.