- Exemple 1 -

Lieu des foyers des coniques dont on connait la directrice et deux points

Le lieu recherché ici est trés simple, l'intérêt de cet exercice est dans la visualisation avec Cabri de la discution du type de conique selon la position du foyer sur ce lieu.

En ce qui concerne la transformation en Cabri-construction de la discution, on sera amené à utiliser un argument de géométrie logique comme présenté dans la parti Alice du site.

La figure est élémentaire à construire. Vous aurez besoin de la macro standard sur les coniques monofocale pour finir la figure :

La macro CnkDFA1.mac qui construit la conique à partir des objets initiaux D, F, et un point de la conique.

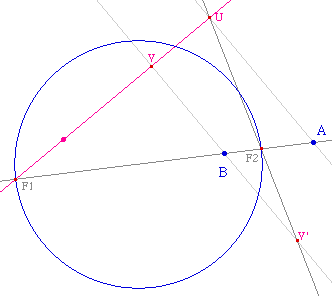
Le lieu des foyers

Si on note U et V les projections orthogonales de A et B sur la directrice, on a la relation d'excentricité : D'où on a : Ainsi, si la droite (AB) est parallèle à la directrice, cette constante est égale à 1, le lieu de F est la médiatrice de [AB]. Si non, le lieu est un cercle d'Appolonius, comme construit ci-contre par les arguments de barycentre, ou plus simplement d'homothétie. On observera que la figure est correcte si A et B sont de part et d'autre de la droite. Nous allons maintenant dégager sur ce lieu les régions pour lesquelles la position de foyer va engendrer chaque type de conique. Le cas général sera traité en premier. Le cas particulier de la médiatrice sera abordé ensuite.

Séparation du lieu par type de conique

Il est clair que la conique sera une ellipse si et seulement si le point F vérifie de plus AF/AU < 1, c'est-à-dire si F est strictement à l'intérieur de cercle de centre A passant par B. Autrement dit si F appartient à un arc de cercle ouvert sur le lieu solution précédent. De même, la conique sera une parabole si F est l'une des extrémité de cet arc : intersection du cercle de diamètre [F₁F₂] précédent et du cercle de centre A passant par U (ou du cercle de centre B passant par V). Ce qui donne :

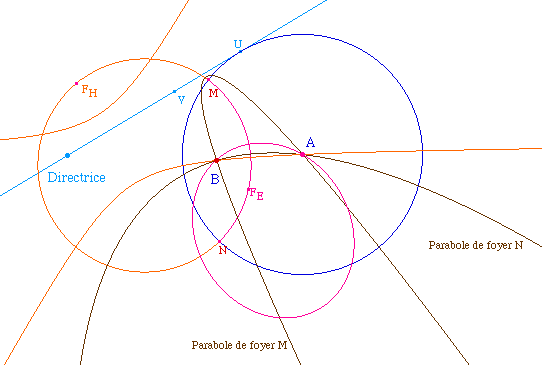
Nécessité d'un argument de géométrie logique

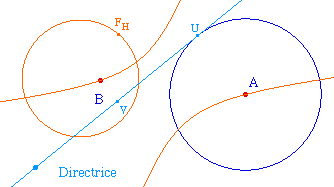
En effet, le cas de l'hyperbole est légèrement différent : la conique est une hyperbole si, comme dans l'illustration ci-dessus, le foyer est dans l'autre arc de cercle que celui construit pour l'ellipse (interieur du cercle de centre A passant par U). Mais la conique est aussi une hyperbole si les deux cercles sont disjoints, comme ci-contre. Ce qui est toujours le cas quand A et B sont de part et d'autre de la directrice, mais aussi possible quand ils sont du même côté.

Pour traiter correctement la situation, il suffit de dire qu'il y a hyperbole quand le foyer est extérieur au cercle (C) de centre A passant par U. Sur un point F_H du cercle lieu des foyers, on applique la macro logique Extérieur Cercle, au cercle (C) et au point F_H. Et c'est seulement à partir de ce foyer logique (crée sous F_H) que l'on construit la conique.

Ainsi, le point F_H existe sur tout le cercle, mais l'hyperbole, elle, n'existe que quand ce point est extérieur du cercle (C).

Lancer la figure LieuFoy1.fig illustrée ci-dessus, avec le traitement logique de l'hyperbole.

Il est par exemple intéressant de déplacer le point F_E aux extrémités de l'arc pour voir l'ellipse associée devenir l'une des deux paraboles de la figure.

On peut aussi, dans le cas d'intersection des deux cercles, prendre un point sur objet F_H de l'arc de cercle qui réalise une hyperbole. Alors quand ce point atteint les extrémités M ou N, l'hyperbole devient elle aussi l'une des deux paraboles de la figure, ce qui n'est pas possible avec le point F_H de la figure proposée en téléchargement.

Le cas particulier où (AB) est parallèle à la directrice.

On l'a dit, le lieu des foyers est alors la médiatrice de [AB] privée de son intersection avec la directrice. On peut alors partager cette droites en trois régions qui deviennent : un segment ouvert pour l'ellipse, les extrémité de ce segment pour la parabole et l'extérieur (ouvert) du segment pour l'hyperbole.

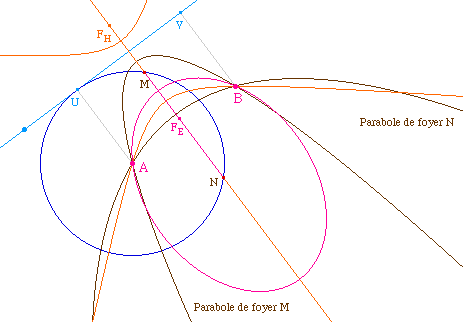
Traitement logique de l'hyperbole

Comme ci-dessus, si le cercle de centre A passant par U ne coupe pas la médiatrice, tous les points de la droite sont le foyer d'une hyperbole. En pratique, on utilisera la même macro logique Extérieur Cercle pour réaliser correctement la figure.

Lancer la figure LFCasMed.fig traitée logiquement.

Remarque : Le point F_H devant parcourir la droite, l'extrémité des demi-droites ne peut-être traitée pour obtenir une parabole : il faudrait prendre des points sur objet des demi-droites pour qu'à l'extrémité le Cabri-point sur objet devienne le point extrémité de la demi-droite..

A propos du passage à l'infini dans Cabri II

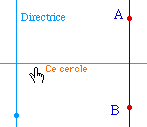
On a déjà fait remarquer que Cabri II gère particulièrement bien l'infini. On peut l'observer à nouveau cette fois en remarquant que si la droite (AB) est parallèle à la directrice, le cercle existe toujours et devient de rayon infini, c'est-à- dire devient la médiatrice de A et B (ceci car on avait pris, dans la première figure, le cercle de centre le milieu de [F1F2] et passant par F2). On se retrouve donc dans la situation précédente.

Mais nous n'avons pas utilisé cette possibilité dans la figure précédente, ce qui lui aurait pourtant donné un caratère général d'unicité de traitement. Ceci à cause du problème déjà détaillé dans la page Manipulation sur D, F, e de la page d'introduction : si on prend un point sur objet du cas infini (cercle-médiatrice) non seulement il n'existe pas dans l'autre cas par retour au fini, ce qui déjà nuit à l'unité de traitement de la figure, mais surtout il n'existe plus, sur le cas infini, aprés un aller retour par le cas fini : une figure contenant le cas fini des coniques à centre et le cas du passage à l'infini (du centre) de la parabole, même enregistrée sur la parabole a sa partie "infini" qui disparaît par passage au cas fini.

En attendant une version de Cabri II qui corrige ce problème, minime certes sur l'ensemble du logiciel, mais dommageable pour un traitement général et unificateur des exercices sur les coniques, abraCAdaBRI propose une macro générale qui traite les deux cas, mais séparément : avec un cercle et une droite. La réalisation est basé sur l'utilisation de la macro Parall.mac qui rend compte du parallélisme de deux droites, construite dans la rubrique Incidences d'Alice et déjà utilisée sur les coniques monofocales lors de la présentation de la construction de la tangente en un point. On notera qu'ici, il a fallu aussi faire disparaître le cercle dans ce cas : il a suffit de prendre le cercle passant cette fois par F₁ au lieu de F₂.

Charger la macro Lieu des Foyers de Cnk par D, A et B (fichier "LFCnkDAB.mac") qui renvoie le lieu des foyers d'une conique de directrice donnée et passant par deux points donnés.

Rappel : Les deux lieux construits sont deux objets bien distincts, ce qui n'aurait pas été le cas avec le "cercle-médiatrice" de rayon infini.

Reste que tout ceci n'est pas bien grave car, en dehors d'une directrice horizontale ou verticale, avoir la droite (AB) parallèle à la directrice relève presque du cas d'école, et s'avère de toute façon un évènement d'une probabilité trés faible. Si un patch de correction devait être disponible sur le serveur de l'Imag lors d'une mise à jour, les pages contenant cette situation seront réécrites.

Menu général