|
|
Une première utilisation
peut-être orientée autour de la calculatrice de
Cabri pour observer des comportements que, selon le
contexte, on attend ou que l'on souhaite
introduire.
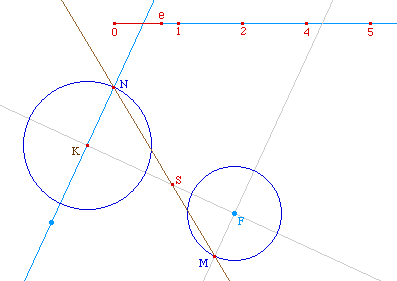
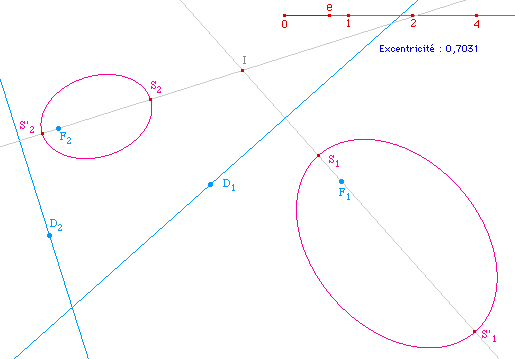
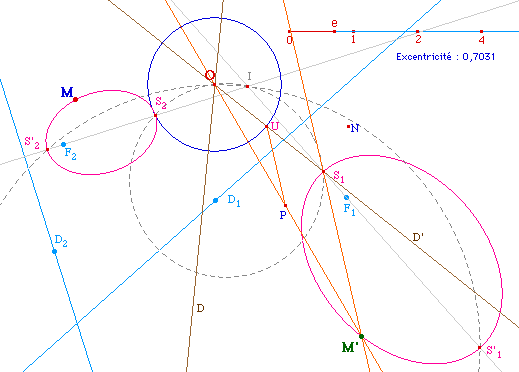
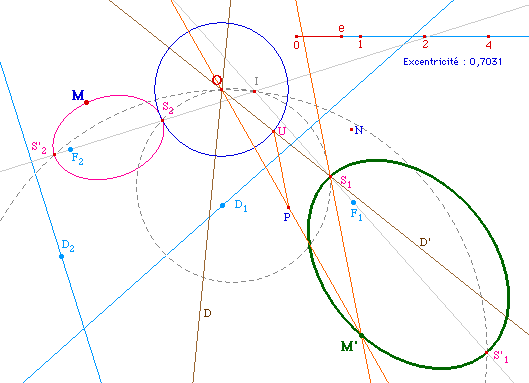
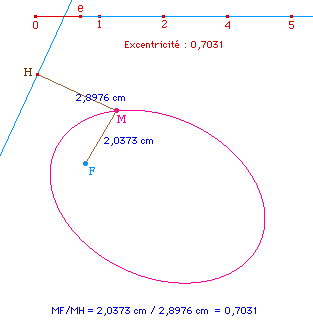
On peut alors observer
différents types de conique ... différents
invariants ...
Note technique :
On remarquera qu'un
arrêt sur la parabole supprime le point M, et donc les
calculs associés. Si, réciproquement, on met
un point sur objet de la conique dans le cas e=1, ce point
sur objet n'existe pas quand on revient à une valeur
différente de 1.
Manifestement Cabri semble avoir (parfois) un
problème de passage à l'infini des points sur
objet lorsqu'une conique passe du cas non
dégénéré au cas
dégénéré de la parabole (en
termes de forme quadratique).
|