Introduction 1 - Macro par cercles associés

La transposition informatique des coniques retenue dans Cabri II étant celle d'un objet défini par 5 points, on se propose de construire une telle Cabri-conique à partir de la définition par directrice et foyer.

Rappelons que, dans cette définition, une conique de foyer F de directrice associée D et d'excentricité e est l'ensemble des points M de la ligne de niveau MF/MH = e où H est la projection orthogonale de M sur D.

Cercles associés à une droite dans un rapport donné

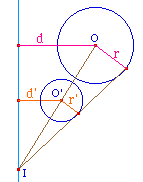
On considère un cercle de rayon r, dont le centre est à une distance d d'une droite. Ce cercle et cette droite sont dits associés dans le rapport r/d. Il est clair que deux cercles, de centres O et O', associés dans le même rapport à une droite D se déduisent l'un de l'autre soit par translation si la droite (OO') est parallèle à D, soit par homothétie comme illustré ci-contre.

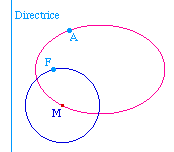
La définition d'une conique par foyer et directrice peut se lire aussi en terme de cette association. On a alors immédiatement le résultat suivant : Une conique de directrice D, de foyer F et d'excentricité e est l'ensemble des centres des cercles passant par F associés dans le rapport e à la droite D. Ce sont ces deux propriétés qui sont à l'origine de la construction point par point à partir d'un cercle associé dans le rapport e à la directrice.

Une première exploration

On se propose ici de construire, par l'outil lieu de point de Cabri, la conique de directrice D, de foyer F et passant par A. On commence par construire un cercle associé dans le rapport e = AF/AH à D où H est la projection orthogonale de A sur la directrice.

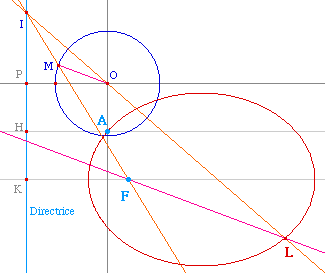
La construction de ce cercle est réalisée à partir des éléments de la figure pour pouvoir être transformé ensuite en macro. Sur cette figure, on a construit P le symétrique de K par rapport à (AH). Le centre O du cercle est l'intersection de la parallèle à la directrice passant par A et de sa perpendiculaire en P. À partir d'un point M du cercle on construit I, intersection de (FM) et de la directrice. D'après ce qui précède, le point L, homothétique de O dans l'homothétie de centre I qui transforme M en F, est un point de la conique cherchée. Seuls deux points de la conique ne sont pas atteints par cette construction, quand M est sur la droite (AO), ce qui est sans incidence sur le tracé du lieu de L quand M parcourt le cercle. CAssExpl.fig On observera par exemple les positions de M qui donnent des points particuliers de la courbe comme le sommet. On vérifiera que la construction est valide, même quand A est sur l'axe focal.

Réalisation de la macro associée

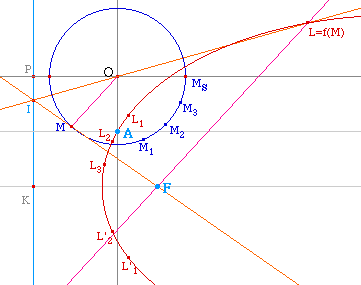
Pour réaliser une macro de Cabri-conique par directrice, foyer et un point, il suffit d'appliquer la construction précédente (transformée en macro) à trois points du cercle et prendre le symétrique de deux de ces points par rapport à l'axe focal. Pour que cela suffise réellement, on prendra soin d'éviter de choisir le point MS ci-dessous qui a pour image le sommet de la conique : si A est sur l'axe focal, c'est déjà ce sommet, la macro ne donnerait plus de conique. On évitera d'une manière générale les points trop particuliers. Ici les trois points retenus M1, M2, et M3 sont obtenus par bissectrice successive à partir de l'angle AOMS.On obtient ainsi trois points L1, L2, et L3 que l'on complète par les symétriques L'1 et L'2 des deux premiers par rapport à l'axe focal (FK). CnkDFA1.fig

Charger la macro Conique par Dir. Foyer 1 pt (CA) (nom de fichier CnkDFA1.mac) d'objets initiaux la directrice, le foyer et le point A par lequel passe la conique.

Tests de robustesse de la macro

Le point A sur l'axe focal

On observera, en prenant une directrice horizontale ou verticale, que la macro fonctionne correctement avec A sur l'axe focal.

Le comportement sur les paraboles

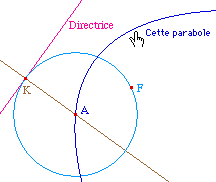
À partir d'une droite D et d'un point A, construire le cercle de centre A et tangent à la droite. Soit F un point sur objet de ce cercle. Appliquer la macro à D, F, A. On obtient une parabole. Redéfinir alors F comme point de base. En déplaçant le point, la conique devient une ellipse ou une hyperbole. Redéfinir à nouveau F comme point sur objet du cercle, la conique redevient une parabole.

Pour le plaisir : avec des hyperboles équilatères

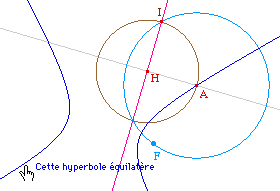
Il ne s'agit pas de tester la robustesse de la macro, mais juste d'illustrer la qualité de Cabri II. Le cercle de centre H passant par A coupe la droite - destinée à devenir directrice - en I. Un point F du cercle de centre A passant par I est le foyer d'une conique de directrice D passant par A qui est toujours une hyperbole équilatère, de par son excentricité (racine carrée de 2). Cabri II le reconnaît...

Menu général