|
|
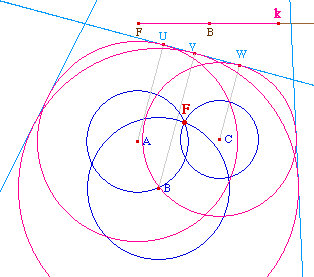
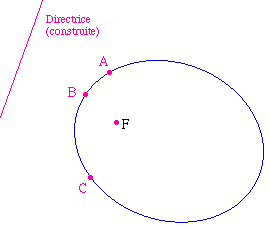
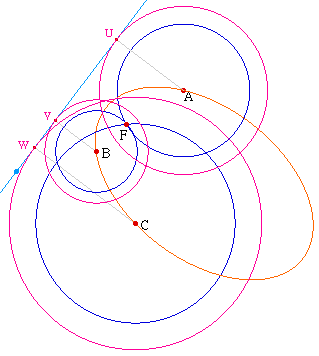
Sur une conique déjà
construite, on a fait apparaître les cercles de centre
A, B, C passant par F et ceux tangents à la
directrice.
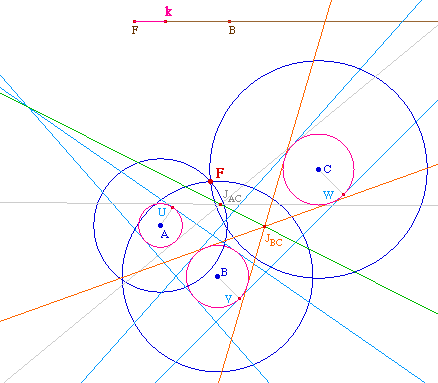
De par la définition des
coniques par foyer, directrice et excentricité, il
est clair que chaque cercle "de
départ" - passant par F - a son rayon
multiplié par une constante (l'inverse de
l'excentricité) pour devenir tangent à la
directrice.
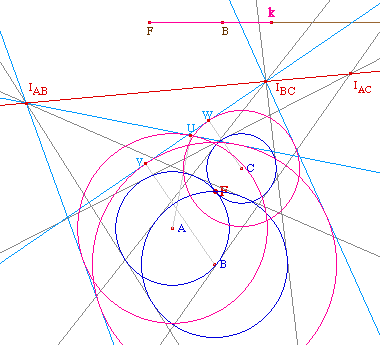
Autrement dit, à partir des
cercles de centre A, B et C, passant par F, on est
amené à cherche un agrandissement (au sens
large) de chacun de ces cercles, de même coefficient,
afin que les cercles ainsi modifiés soient tangents
à une même droite.
|