En notant encore U et V les
projections orthogonales de A et B sur la directrice, et W
celle de C, les constructions vues à la page
précédente aménent tout naturellement
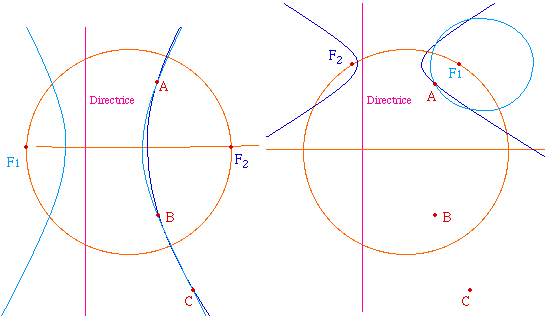
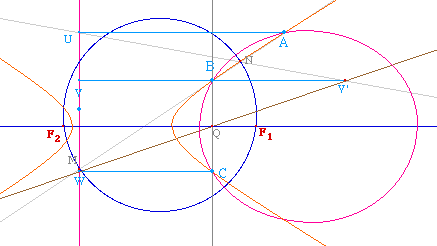
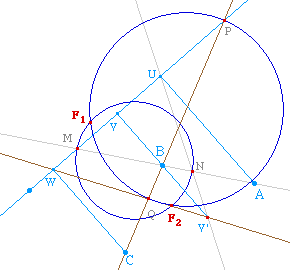
à la figure ci-contre : pour passer par A et B, le
foyer doit être sur le cercle de diamètre
[MN], et pour passer par B et C il doit aussi
être sur le cercle de diamètre [PQ]. On
exclu ici le cas particulier où l'une des trois
droites (AB), (BC) ou (AC) serait parallèle à
la directrice : le cercle serait alors remplacé par
la médiatrice des deux points
concernés.
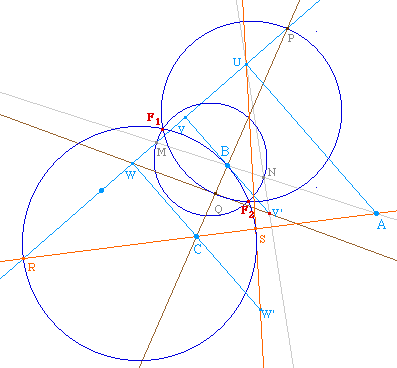
On peut s'amuser à verifier que le troisième
cercle, de diamètre [RS] construit à
partir des points A et C est bien concourant aux deux
autres, comme ci-dessous :
|
|
On observera par ailleurs qu'il peut ne pas y avoir de solution : les cercles peuvent être soit disjoints, soit l'un contenant l'autre, selon les positions des points et de la droite.À partir des deux foyers possibles F1 et F2, on applique la macro de tracé de Cabri-conique :
|