Tangente 3 - Tangentes issues d'un point

Dans cette page nous utiliserons la propriété focale des tangentes : l'angle droit en F du triangle IMF où I est l'intersection de la tangente en M et de la directrice associée au foyer F.

Nous utiliserons aussi la construction point par point de la conique par l'intermédiaire d'un cercle associé dans le rapport e à la directrice.

Compléments sur les cercles associés

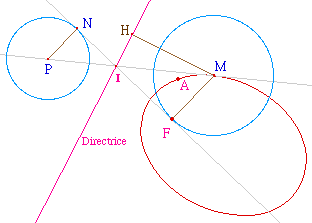
La définition des cercles associés à la directrice dans le rapport e d'excentricité, et la propriété d'orthogonalité du triangle MFI rappelée ci-dessus donnent ensemble immédiatement le résultat suivant : Une droite D coupant la directrice en I est tangente à la conique (de foyer F d'excentricité e) si et seulement si la droite (IF) est tangente à un cercle centré sur cette droite D et associé à la directrice dans le rapport d'excentricité. En effet, c'est clair si le centre M du cerle appartient à la conique : on retrouve la CNS de l'orthogonalité en F de IMF. Sinon, si le centre est un point P de la droite D, on conclu par l'homothétie de centre I qui envoie P en M.

Application à la situation

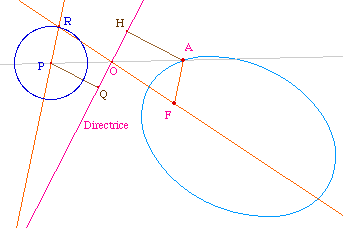
Soit un point P à partir du quel on souhaite construire les tangentes à la conique. Ce qui précède nous invite à construire, dans une première étape, le cercle de centre P associé à la directrice dans le rapport d'excentricité. Cela se fait par une simple homothétie comme ci-contre. On obtient le cercle de centre P passant par R. Figure partielle TgtIssu1.fig correspondant à cette première étape.

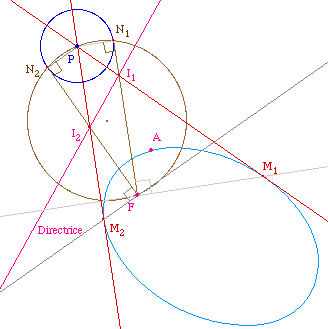
Pour que (PM), coupant la directrice en I soit tangente à la conique, il faut que le cercle soit tangent à (IF). Le cercle étant donné, il suffit de construire ses tangentes issues de F. On obtient deux points de la directrice possibles, I1 et I2, qui amènent par homothétie, à deux points de contact M1 et M2 de la conique. Remarque : Comme dans la page précédente, la présence de la conique sur cette figure est inutile pour la construction. Elle n'est là que pour vérifier de visu que l'on a bien construit une tangente à la conique définie par D, F et le point A : M1 et M2 sont construits par intersection de deux droites et non pas une droite et la conique. Figur finale TgtIssu2.fig. Charger la macro Tangente issue d'un point à une conique "monofocale" associée (fichier "TgtIssu1.mac").

 

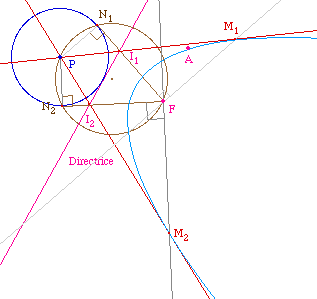
Et la parabole ?

Contrairement à la page précédente sur les tangentes parallèles à une droite donnée, ici la situation est exactement la même que dans le cas des coniques à centre : l'existence d'un centre n'apportant pas de situation symétrique, il n'y a de pas perte quand celui-ci disparaît. TgtIssu3.fig spécifique à la parabole.

Menu général