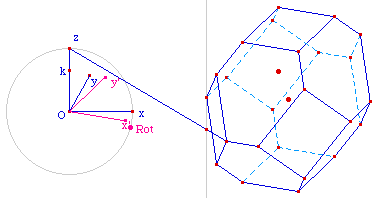
|
|
On part d'une figure qui comprend déjà le traitement opaque de la première branche, du cube au cuboctaèdre, que l'on place en position de seconde branche. Comme dans la première partie, les arêtes de la face supérieure sont toujours visibles.
|
|
|
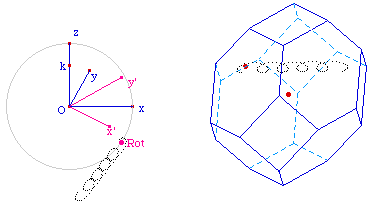
On part d'une figure qui comprend déjà le traitement opaque de la première branche, du cube au cuboctaèdre, que l'on place en position de seconde branche. Comme dans la première partie, les arêtes de la face supérieure sont toujours visibles.
|
|
|
Le traitement se fait comme les faces octogonales de la première branche, l'illustration ci-dessous est désormais une "classique" de la gestion des faces cachées.La macro, d'objets initiaux les 6 points de la face, en partant de celle supérieure gauche, et le point z, construit les segments visibles par l'adjonction de 3 points conditionnés à l'existence de l'intersection droite / segment. |
 |
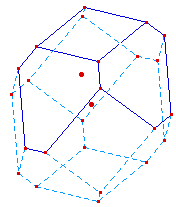On peut faire la figure, ou encore
|
 |
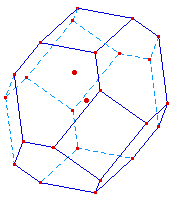En réalité, la même macro Face Hexa Visible s'applique encre aux faces inférieures. Il suffit donc de l'appliquer à nouveau 4 fois.On peut aussi directement
|
|
|
En réalité, la même macro Face Hexa Visible s'applique encre aux faces inférieures. Il suffit donc de l'appliquer à nouveau 4 fois.On peut aussi directement
|
On crée par exemple deux
points conditionnés à l'intersection sur deux
sommets opposés du carré, cela suffit à
construire les 4 faces du carré. Les deux de gauche
servent à l'apparition à gauche, et celles de
droite à la disparition de la face à
droite.
Charger la macro
FaceCarre.mac
(Face Carrée Visible) pour
l'appliquer à la figure
précédente.La figure est alors
terminée.
Charger la figure TrSOpk09.fig
finale (avec les points de construction).
Charger la figure TrSmOpak.fig
finale nettoyée des points de
construction.
Menu général
