La Galerie
d'Alice
5 - Troncature opaque du cube
par les arêtes
[Introduction
à la géométrie logique] [Les
macros logiques] [Premiers
exemples significatifs]
[Les Incidences
d'Alice] [Constructions
spécifiques] [Retour
Alice] [Menu
général]
La figure de troncature
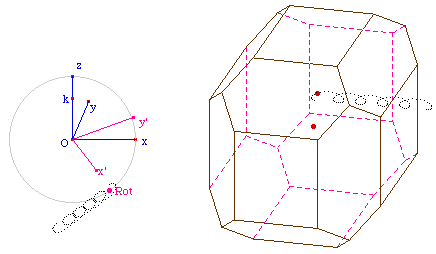
 Charger la figure TrAOpkF.fig
finale.
Charger la figure TrAOpkF.fig
finale.
On peut consulter les
détails de sa construction, en 4
étapes, avec 3 macro-constructions
appropriées.
Deux figures complémentaires sont
aussi disponibles ci-dessous.
Complément : troncatures
simultanées
Sur la figure précédente, on
coupe à nouveau les anciens sommets (du cube) par les sommets,
la troncature étant toutefois limitée en amplitude par
celle faite par les arêtes. On a donc une troncature double du
cube : par les arêtes et les sommets.
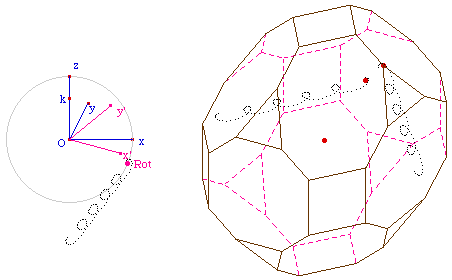
 Lancer la figure TrArtSom.fig
de cette double troncature.
Lancer la figure TrArtSom.fig
de cette double troncature.
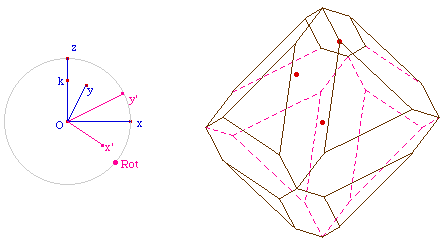
Illustrations de la troncature double
Sur le dessin suivant, la troncature par
les arêtes est maximale (dodécaèdre rhombique),
et on opère une troncature partielle par les sommets
:
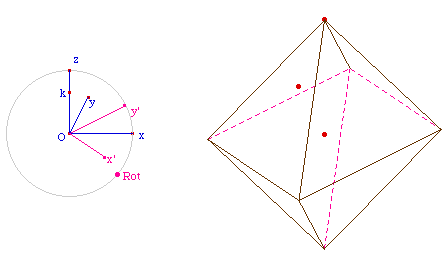
Sur ce dessin suivant, on reste dans la
troncature maximale par les arêtes, et on y ajoute une
troncature, elle aussi maximale, par les sommets : on retrouve alors
l'octaèdre.
Cas particulier de la troncature double
Quand, dans une troncature par les
arêtes, on tronque aussi par le sommet, au maximum des
possibilités offertes par la première troncature, on
obtient un autre type de polyèdres qui a la
particularité de produire, pour une
position précise de cette
troncature, un polyèdre semi-régulier : le petit
rhombicuboactaèdre, proposé ici en faces
opaques.
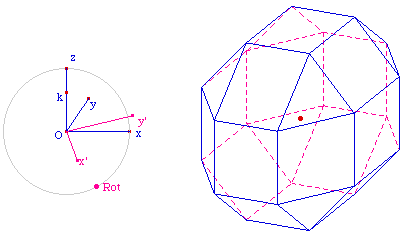
 Lancer la figure RhCuboOp.fig
du petit rhombicuboctaèdre opaque.
Lancer la figure RhCuboOp.fig
du petit rhombicuboctaèdre opaque.
[Introduction
à la géométrie logique] [Les
macros logiques] [Premiers
exemples significatifs]
[Les Incidences
d'Alice] [Constructions
spécifiques] [Retour
Alice] [Menu
général]
 Menu général
Menu général





