Troncature d'un cube par les arêtes

On se propose, sur cette page, de détailler la construction d'une troncature du cube par les arêtes. La figure est facile à réaliser et peut faire l'objet d'activités d'élèves, sur le thème des intersections de plans, à partir de la rotation du cube.

La page se termine par un complément où l'on ajoute une troncature les sommets sur celle commencée par les arêtes.

La figure de départ

Définition de la troncature

 

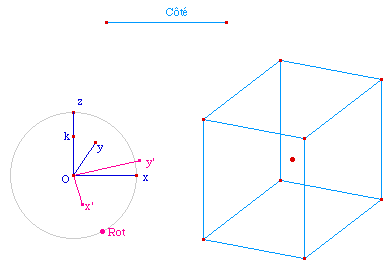
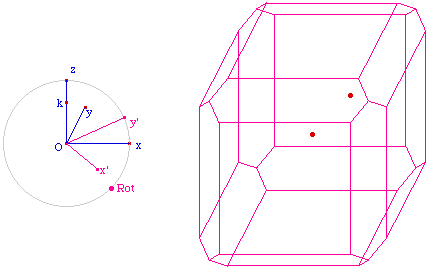
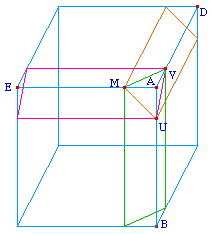
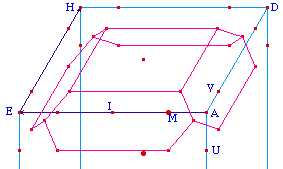
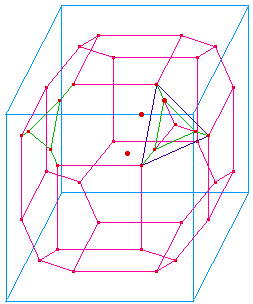
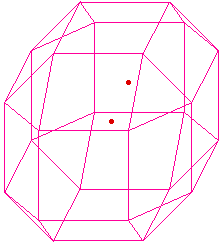
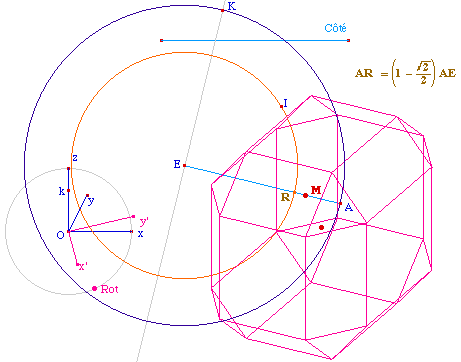
Quand on réalise une troncature par les sommets, on coupe chaque sommet selon un plan orthogonal à la diagonale du cube passant par lui, on obtient un triangle équilatéral (comme MUV). Tronquer par les arêtes, c'est couper chaque face contenant le sommet par trois plans, chacun paralléle à une des arêtes, et ceci de manière invariante par permutation sur ces arêtes. 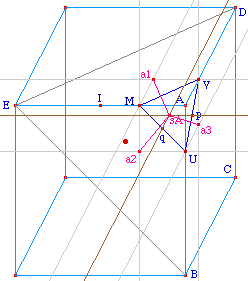Cela revient à tronquer chaque face par un plan qui lui est orthogonal et qui reprend la trace de la troncature par les sommets, pour des raisons d'invariance par rotation d'axe la diagonale du cube passant par ce sommet : Ainsi au lieu de couper le sommet par le plan (MUV), on découpe les faces selon les segment [MU], [MV] et [UV] dans les directions orthogonales aux faces, donc définies par les arêtes respectives [AD], [AB] et [AE], d'où l'expression de troncature par les arêtes.

Macro Troncature Arete

 

Il est clair, dès le schéma précédent, que les intersections des plans deux à deux donnent les points des faces du cube qui sont un sommet du nouveau polyèdre. Reste à construire le sommet manquant, qui est à l'inersection des trois plans. Il est facile de voir que les droites passant par les milieux des côtés du triangle MUV et parallèles aux arêtes opposés sont concourantes (là encore pour des raisons de symétrie). On obtient ainsi le point sA par l'intersection de deux d'entre elles. On peut alors faire une macro construction qui, à partir des trois points M, U, V et des segments qui les portent, [AE], [AB] et [AD], donne les trois segments cherchés [a1 sA], [a2 sA], et [a3 sA]. On peut aussi choisir de : La figure TrCbArt1.fig pour faire la macro.

Application à la partie supérieure

 

En utilisant les vecteurs AE et EH, il est facile de reproduire les positions des points MUV aux trois autres sommets de la face supérieure. On applique alors trois fois la macro précédente. Pour relier les points, il est plus facile de placer la face en position frontale, en faisant tourner le cube par le point Rot.

Fin de la construction

Propriété de la troncature

Au maximum de la coupe, quand M est en I, les carrés disparaissent, on arrive alors au dodécaèdre rhombique, polyèdre composé de 12 losanges identiques - comme son nom l'indique - qui a la particularité de paver l'espace. On remarquera ausi qu'il n'y a pas de position du point M pour laquelle le polyèdre obtenu soit semi-régulier. En effet, même si on peut facilement obtenir la position du point M pour que toutes les arêtes du polyèdre aient la même longueur, les faces hexaagonales ne sot pas régulières (par exemple non inscriptibles dans un cercle).

On peut également redéfinir M comme point sur objet de (toute) l'arête [AE]. On verra alors que dans la seconde partie de l'algorithme, il ne se passe pas de phénomène particulier : on conserve un homothétique du dodécaèdre rhombique obtenu quand M est en I qui tend vers le centre du cube.

Complément : ajout d'une troncature par les sommets

En effet, il est tentant de se donner un point sur objet d'une des arêtes obtenue à un sommet du cube lors de cette troncature, et de tronquer selon le sommet : il y a un triangle équilatéral (en violet ci-contre) et l'on tronque selon un homothétique de ce triangle à partir d'un point sur objet. On remarquera qu'ici la troncature maximale ne dépasse pas les arêtes obtenues par la troncature précédente. Ce serait possible, mais ce sera l'objet d'une autre figure, et donc d'une autre fiche. Une fois un coin fait, on termine facilement les sommets haut, et par symétrie centrale du cube ceux du bas, comme pour la première troncature.

 

Enfin, en redéfinissant le second point de la troncature par sa position maximale du triangle équilatéral de ci-dessus, on obtient un cas particulier de cette double troncature. La figure ArtSomMX.fig de ce cas particulier. On observera qu'il existe une position particulière du point de troncature - qui n'est plus une troncature par les arêtes - pour laquelle le polyèdre obtenu est semi régulier : c'est le petit rhombicuboctaèdre. Nous en reparlerons dans les (futures) pages sur les polyèdres semi-réguliers, mais il est tentant de le construire sur cette figure : Il suffit de redéfinir le point M comme étant le point R décrit sur la figure ci-dessous :

On peut alors proposer, par la rotation, une vérification expérimentale que le solide a bien ses arêtes toutes de même longueur. En effet quand un carré d'une face du cube est dans un plan frontal, les arêtes des rectangles "obliques" de droite (pour faire rapide) sont aussi dans un plan frontal, donc en vraie grandeur. On peut ainsi vérifier si elles ont même longueur ... ce qui est le cas comme sur l'illustration ci-contre ... Lancer une figure RhombiCb.fig du petit rhombicuboctaèdre (figure optimisée par rapport à la précédente).

Les diverses troncatures de cette page font l'objet d'un traitement des parties cachées dans une rubrique Alice qui leur est consacrée.

début

Menu général