Géométrie dans l'espace

Rotation de solides en perspective cavalière

[Cas particulier du cube] [Cas particulier du paraboloïde hyperbolique]

[Plans d'objets en vraie grandeur] [Troncature du cube par les arêtes]
[Retour Espace"] [Menu général]

On se propose, sur cette page, de s'intéresser à la rotation dans l'espace de divers objets, en particulier les solides, selon un axe vertical. La méthode utilisée, développée dans le premier paragraphe, est accessible en classe de première, voire en seconde, dans le cadre d'un club-Cabri.

Certaines figures qui en découle peuvent être plus longues à réaliser : ce site est aussi fait pour télécharger les figures des collègues. Aussi, si vous faites des constructions sur la base de cette page, penser à les proposer pour qu'elles trouvent leur place ici ...

Rotation d'un trièdre en perspective cavalière

Le plan (xOz) est le plan frontal de la perspective. [Oy) est la fuyante. (O, x, y, z) est un trièdre orthonormé de l'espace. On a pris k comme point sur objet de [Oz]; c'est le coefficient de réduction. y est alors pris sur objet d'un arc de cercle de centre O passant par k. On peut ainsi faire varier indépendament le coefficient de la PC ou son angle de fuite.

Remarque : le point y a été pris sur un quart de cercle pour une gestion plus simple des parties cachées dans les rubriques Alice consacrées à cette question. Si, dans une des figures de cette page, on désire un angle de fuite négatif, ou supérieur à un angle droit, on peut redéfinir y comme point sur le cercle support de l'arc.

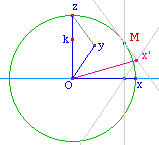
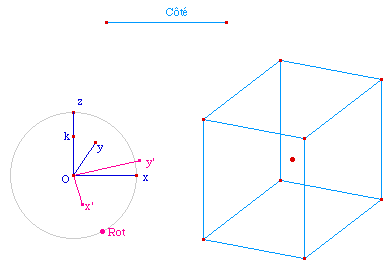
M est un point du cercle frontal. On veut tracer sa projection sur (xOy) dans la perspective ainsi définie.

Plusieurs arguments sont possibles : dans l'espace avec le quart de tour d'axe (Ox) qui envoie z sur y, dans le plan avec l'affinité de base (Ox) qui envoie z sur y.
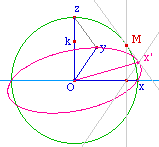
Dans les deux cas, on peut construire l'image x' du point M par un simple argument homothétique. Sur la figure ci-contre, on a pris soin de ne pas utiliser la droite (Mz), qui n'existe pas quand M est en z, afin que les figures construites à partir de ce trièdre de référence existent toujours : on a pris des parallèles aux côtés du triangle zOy.

En construisant le lieu de x' quand M décrit le cercle, on a l'image du cercle de centre O passant par x - du plan (xOy) - dans cette perspective. On remarque que, sauf si y est en k (et on a alors une vue de face) la conique n'est pas contenue dans le cercle. Cela signifie en particulier que l'image d'une sphère en perspective cavalière n'est pas un cercle mais bien une ellipse.

La figure RotPC.fig.

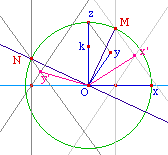
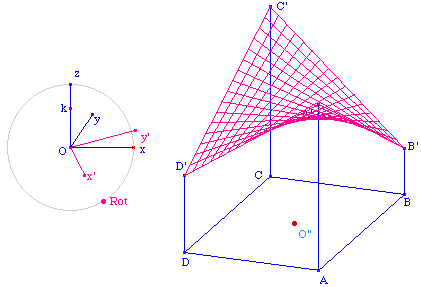
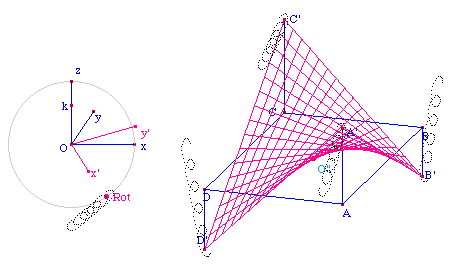
Pour réaliser la rotation d'un trièdre, il suffit de reprendre la construction avec un point N tel que (O, M, N) soit orthonormé direct du plan (xOz). On obtient un point y'. Le repère x'Oy' quand M se déplace sur le cercle, est la repréentation en perspective cavalière du repère xOy autour de l'axe (Oz).
On notera que les rayons [Ox'] et [Oy'] sont conjugués puisqu'image des rayons orthogonaux [OM] et [ON] du cercle par une application affine, l'affinité de base (Ox) qui transforme z en y.

La figure Triedre.fig.

Dans la suite, nous allons nous proposer de faire tourner divers objets. Commençons par une première application très simple.

Rotation d'un paraboloïde hyperbolique

Il s'agit de faire tourner un carré en perspective cavalière, sur la base de la rotation du trièdre x'0y', à une homothétie près. Par les sommets A, B, C, D on trace des segments verticaux, d'extrémité A', B', C' et D'. Puis on partage les segments primés en 16 parties égales, et on joint les points opposés correspondants.

ParaHyp.fig

Mode d'emploi de la figure

La figure tourne par l'annimation du point Rot

Le carré de base est déplaçable par O" et sa taille est modifiable par le point A.

Les extrémités A', B', C' et D' peuvent aussi être animés. Pour cela ce sont des points sur objet de segments.

Ces segments sont de même taille, réglés par des points cachés DMax et DMin, sur la droite passant par D.

On peut animer simultanément les 5 points A', B', C', D' et Rot, dans des sens différents. Il peut aussi être intéressant de ne conserver que la grille et de cacher aussi les supports des points.

On peut aussi consulter les détails de la construction.

Hyperboloïde à une nappe

Il s'agit ici d'utiliser la rotation d'un repère pour simuler la fabrication filaire d'un hyperboloïde par la rotation d'un cercle par rapport à un autre, relié par des fils. Dans les réalisations matérielles, on utilise en général deux disques de carton.

Sur cette figure le disque du haut est fixe, celui du bas tourne avec le point Rot. Comme les fils sont rigides, le disque du bas remonte (point H). Contrairement à la réalité, où les fils s'emmèlent au bout d'un demi-tour, ici ils se décroisent. Pour la manipulation, il est intéressant de faire une animation du point Rot.

Hyperbol.fig

Remarque : la figure proposée ici a été faite avec Cabri I, et simplement traduite en version II. Il est clair qu'elle n'est pas du tout optimisée pour Cabri II, et il serait intéressant de la refaire entièrement, en utilisant les outils de la nouvelle version.

Rotation d'un cube

Cette construction est la principale de la page, car elle sera réutilisée dans le site pour toutes les constructions de polyèdres réguliers ou semi-réguliers qui se font à partir du cube, ainsi que leur troncature : ces constructions seront directement faites sur un trièdre en rotation.
On s'est donc attaché, en particulier, à ce que la construction du cube soit toujours définie.

RotCube.fig

On peut aussi s'intéresser aux principes de la construction.

On a choisi d'utiliser un curseur pour la taille du cube. On aurait pu avoir un comportement plus en manipulation directe, comme avec le paraboloïde hyperbolique. On a préféré garder la manipulation directe sur le cube - ou sur les objets construits à partir de lui - pour les différentes troncatures qu'on y ajoutera par la suite.

Bien-sûr, la rotation d'un cube en perspective cavalière amène la question de la gestion des parties cachées : peut-on, dans un environnement de géométrie dynamique, aborder le tracé en faces cachées à la règle et au compas ? La réponse est oui.

Toutes ces questions de parties cachées sont traitées dans des rubriques d'Alice, ici pour celle du cube, et là pour celle des troncatures.

Un exemple (temporaire) d'une telle gestion

Voici une figure traitant de la section d'un cube par le plan passant par trois points des faces visibles, avec rotation le la section. La construction d'une telle section sera abordée dans une page sur les sections du cube.

TCbSect.fig

Sur cette figure, la section se modifie à partir du cube de référence fixe, puisque des points de base sur le cube en rotation ne pourraient pas tourner en même temps que ce cube.

Remarque : comme pour l'hyperboloïde filaire, cette figure est une traduction en Cabri II d'une figure faite en Cabri 2.1 (Mac). On notera par exemple que certaines sections sur le cube de départ, en gris, ne sont pas effectuées (par manque d'objets). Il serait intéressant de refaire cette figure entièrement en version II.

[Cas particulier du cube] [Cas particulier du paraboloïde hyperbolique]

[Plans d'objets en vraie grandeur] [Troncature du cube par les arêtes]
[Retour Espace"]