|
 La
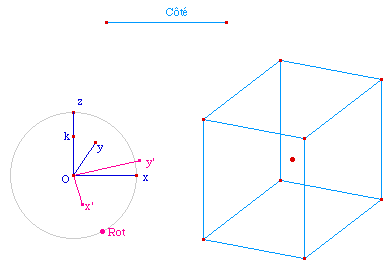
figure RotCb01.fig
dans cet état partiel. La
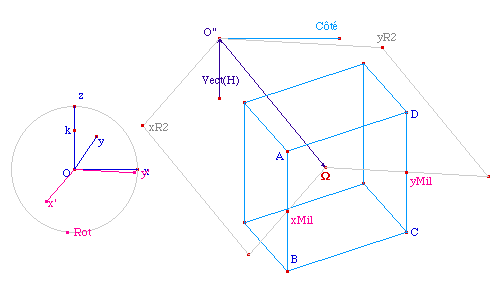
figure RotCb01.fig
dans cet état partiel.
|
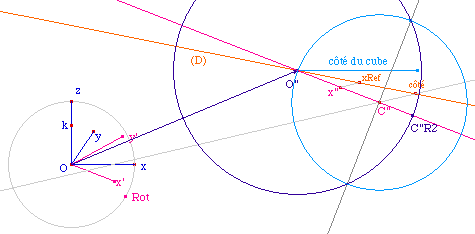
Le problème soulevé
plus haut se présente d'entrée : si on fait
une homothétie à partir d'un segment
horizontal, quand le point Rot passera en x, la construction
de l'homothétique ne fonctionnera plus car les points
seront alignés. On a retenu ici de projeter le tout
(les longueurs de [Ox] et du côté du
cube) sur une droite construite, par bissectrices
successives, de telle façon que les points
correspondants,
x",
et
xRef
ne puissent être confondus pour Cabri, et donc tel que
le point
C",
qui défini l'extrémité de
l'homothétique existe toujours.
Ce point acquis, il faut ensuite
multiplier la longueur O"C" par 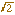 .
On obtient le point
C"R2,
en utilisant deux cercles. .
On obtient le point
C"R2,
en utilisant deux cercles.
On fait ensuite de même avec
l'autre segment [Oy'] du repère tournant (non
illustré sur l'image
précédente).
|