Rotation d'objets

Exemple du paraboloïde hyperbolique

Rappel de l'objectif

Il s'agit de faire tourner un carré en perspective cavalière, sur la base de la rotation du trièdre x'0y', à une homothétie près. Par les sommets A, B, C, D on trace des segments verticaux, d'extrémité A', B', C' et D'. Puis on partage les segments primés en 16 parties égales, et on joint les points opposés correspondants.

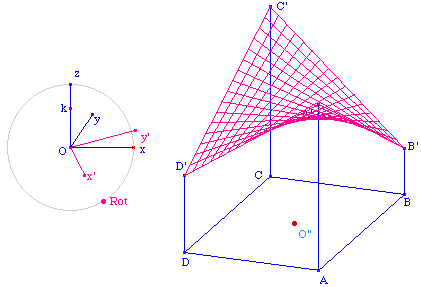
ParaHyp.fig (figure finale)

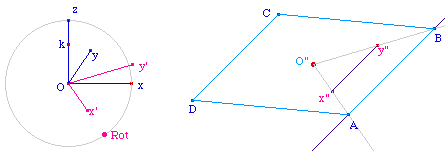
Construction de la base

À partir d'un point O", on commence par translater les segments [Ox'] et [Ox"]. Puis, sur la demi-droite [O"x"), on place un point sur objet A. On construit (O", A, B) l'homothétique du repère (O", x", y").

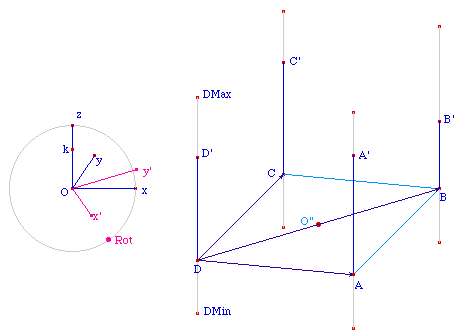
Réalisation des tiges

Sur des parallèles à [Oz] passant par les 4 sommets du carré ABCD, on fixe - ici sur le sommet D - des limites maximales et minimales pour l'évolution des tiges verticales de l'objet, quand ces tiges seront animées. Les points A', B', C', D' sont des points sur objet de ces segments.

Construction de la trame filiaire

On partage le segment [A'B'] e, 16 parties égales, opération que l'on transforme en macro construction pour partager le segment opposé lui aussi en 16 parties égales. Puis on rejoint les points correspondants par un segment.

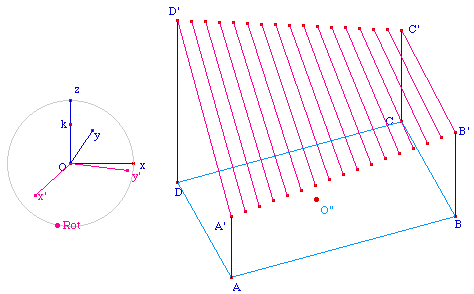
On fait de même pour les deux autres segments [A'D'] et [B'C'], ce qui donne la figure cherchée.

Menu général