|
|
|
En construisant une représentation en vraie grandeur d'une section triangulaire d'un cube, on cherche à faire coïncider les deux triangles, celui en vraie grandeur, et celui en perspective cavalière. Voici les 4 étapes décrites ci-contre :
|
Plans d'objets en vraie grandeur en perspective cavalière
|
|
|
En construisant une représentation en vraie grandeur d'une section triangulaire d'un cube, on cherche à faire coïncider les deux triangles, celui en vraie grandeur, et celui en perspective cavalière. Voici les 4 étapes décrites ci-contre :
|
|
|
|
|
|
|
I et J étant connus, la parallèle à (EG) passant par J coupe (CD) en un point K' qui est la rotation de J d'un quart de tour autour de l'axe (BF). Et donc pour tout point K de (BF), KK' est la longueur de [KJ] en vraie grandeur.Il en résulte que la médiatrice de [JK'] coupe la droite (BF) au seul point K pour lequel KJ est longueur en vraie grandeur du segment [KJ] (non il n'y a pas d'erreur de frappe).On vient donc de construire un
triangle IJK tel que ses côtés sont, sur le
dessin, en vraie grandeur, alors que le plan (IJK) n'est pas
parallèle au plan frontal.
|
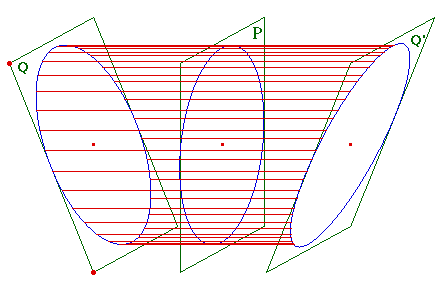 |
Soit C un cercle de plan Q, P un plan orthogonal à la droite D, C' l'image de C dans la réflexion S de plan P (les deux cercles C et C' ont donc même rayon), toute droite parallèle à D (c'est à dire perpendiculaire au plan P) passant par un point M' de C' est globalement invariante par S et repasse donc par le point M=S(M') du cercle C=S(C'). Autrement dit le cercle C' se projette selon le cercle C - qui est de même rayon, donc en vraie grandeur. Or le plan du cercle C', c'est à dire Q' = S(Q), est parallèle au plan Q si et seulement si ils sont tous les deux parallèles au plan P, c'est à dire orthogonaux à la droite D.Ainsi lorsque la projection p n'est pas orthogonale, il existe bien une deuxième direction de plans dont les objets sont projetés en vraie grandeur.Il est alors facile de voir que seuls les plans parallèles à Q et leurs images par la réflexion S possèdent cette propriété. |
|
|
Quelque soit la perspective cavalière (ci-contre déplacer le point D), quand on construit le plan des objets en vraie grandeur passant par I, l'arête de la fuyante (FG) est toujours orthogonale à l'arête du plan frontal (IK). Ou encore sur le dessin en PC de la figure, la fuyante (FG) est une hauteur de IJK.Un joli exercice de géométrie dans l'espace. Il est, n'est-il pas ?
|
[Rotation de solides] [Troncature du cube par les arêtes] [Menu général]