|
|
On a déjà présenté à
la page Plans en Vraie
Grandeur qu'il existe une autre direction de plans que
celle du plan frontal pour laquelle les objets sont en vraie
grandeur en perspective cavalière.
Or on peut faire la remarque suivante :
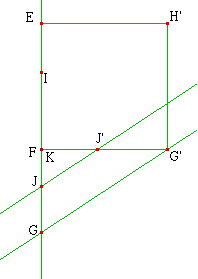
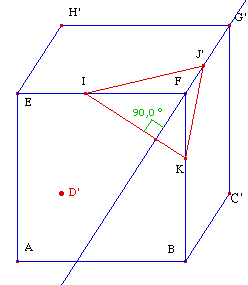
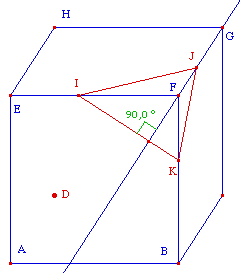
Quelque soit la perspective cavalière (ci-contre
déplacer le point D), quand on construit le plan des
objets en vraie grandeur passant par I, l'arête de la
fuyante (FG) est toujours orthogonale à l'arête
du plan frontal (IK). Ou encore sur le dessin en PC de la
figure, la fuyante (FG) est une hauteur de IJK.
 Lancer
la figure PlanVGPb.fig
d'expérimentation Lancer
la figure PlanVGPb.fig
d'expérimentation
|