On se propose ici de s'intéresser à la construction dans Cabri II du mouvement d'une planète autour d'une étoile de deux manières différentes : par une approximation d'une solution d'équation différentielle, en construisant une ellipse obtenue par 5 points de cette approximation, et par la construction exacte, les deux approches étant possibles avec l'outil Conique de Cabri II

Introduction

L'observation du ciel est une pratique vieille comme l'homme. Les phénomènes observés étaient souvent considérés comme des signes divins et interprètés en accord avec les dogmes religieux existants. Ainsi, le mouvement "chaotique" de certains astres (les planètes) faisant désordre dans le système géocentrique en vigueur chez les grecs, Ptolémée a imaginé un modèle qui décrit le mouvement de ces "astres errants" comme combinaison complexe de plusieurs mouvements circulaires (image ci-contre). Il fallut attendre Képler (1571-1630) pour disposer d'une étude sérieuse sur certaines des lois qui interviennent dans le mouvement des planètes. C'est un peu plus tard et grâce aux lois de Képler que Newton (1642-1727) élabora la loi de la gravitation universelle. 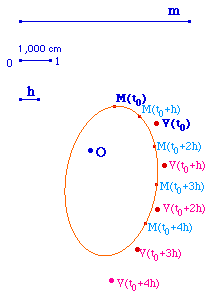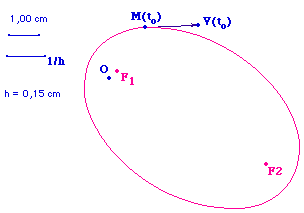Selon la première loi de Képler toutes les planètes effectuent un trajet elliptique dont le soleil est un des foyers. Plus généralement, tout objet subissant une attraction Newtonnienne a pour trajectoire une conique.

Lorsque le nombre d'objet du système considéré comporte plus de deux objets on est obligé de faire appel au calcul numérique et aux ordinateurs, mais les solutions sont alors très sensibles aux conditions initiales ce qui rend l'étude complexe . Nous allons nous limiter à l'étude d'un système composé de deux corps et utiliser la méthode numérique d'euler pour obtenir par discretisation cinq points (M(t_o) compris) qui permettrons la construction de la conique grâce à la fonction Conique de CABRI II.

Rappel sur la Méthode d'Euler

Considérons l'équation différentielle y'(t)=f(t), avec pour condition initiale y'(t₀)=A, où f est une fonction de R dans R. Les fonctions y vérifiant cette équation sont des fonctions réelles à valeurs dans R. Représentons cette solution dans un plan muni d'un repère orthonormé, et considérons le point (t,(y(t)) de la courbe. Au voisinage du point (t,y(t)) la courbe se "confond" avec la tangente. On peut donc estimer qu'à l'instant t+h (h "suffisament" petit) le point (t+h,y(t)+hy'(t)) est "proche" de la courbe cherchée (y'(t)=f(t) étant connue).

En itérant ce procédé on obtient la construction par récurrence d'une suite de points "proches" de la courbe On peut résumer cette construction au schéma de récurrence suivant: U₀(t) = (t,y(t)) et U_k+1(t) = U_k(t)+hU_k'(t), les points proches de la courbe solution du problème étant les points de coordonnées U_k(t₀) (k entier).

Application au mouvement d'un corps soumis à une attraction Newtonienne.

En combinant la methode d'Euler aux lois de la mécanique céleste (la loi de la gravitation universelle), la deuxième loi de Képler et principe fondamental de la dynamique nous allons effectuer un tracé de la trajectoire d'un solide en orbite.

On utilisera sur la feuille CABRI des longueurs de segments pour représenter des grandeurs physiques différentes selon les correspondances suivantes:

Grandeur	Représentation
Vitesse	1cm pour 1 cm / s
Masse	1 cm pour 1 kg
Distance	1 cm pour 1 cm

Notations retenues

Il s'agit de déterminer le mouvement d'un solide M de masse 1kg (assimilé à un point) , soumis a l'attraction newtonnienne d'un solide O de masse m (lui aussi assimilé à un point). Le référentiel choisi est attaché au solide O.
M est lancé à l'instant t₀ avec une vitesse V(t₀) et a un vecteur position r(t₀), d'origine O.
Un point V(t₀) du plan indiquera que V(t₀)=M(t₀)V(t₀).

On notera r(t), V(t) et a(t) ) respectivement les vecteurs de position, de vitesse et d'accélération du point M à l'instant t.

Amélioration de la méthode d'Euler

Le point M étant entièrement décrit à l'instant t par la donnée du couple (vecteur position, vecteur vitesse), nous allons appliquer la méthode d'Euler avec la relation de récurence U_k+1 = U_k + h.U_k', où :

La méthode d'Euler est d'ordre 1, donc peu précise. Or, compte tenu du fait que a(t + hk) est constructible avec Cabri, on peut rendre le système plus précis, et atteindre une précision d'ordre 2, par :

Nous allons maintenant construire avec Cabri les points M₀(t+hk) pour k=1 à 4.

Cabri-construction d'un point. Macro associée

Le vecteur a(t0) de M à l'instant t0 est dirigé de M(t0) vers O et a pour norme m/OM2. On notera a l'extrémité de ce vecteur. On construit alors le vecteur a(t0)*h puis le vecteur a(t0)*h *h/2. Il ne reste plus qu'à placer le point M(t0+h) tel que : et le point V(t0+h) tel que :

La macro précédente Mt0ph.mac d'objets initiaux m (2 points, de gauche à droite) l'unité (idem), le paramètre h (idem), le point O, puis les deux points M(t₀) et V(t₀).

Application de la macro, construction de 4 points et de la conique

On construit ainsi, à partir du point M(to) quatre autres points, en appliquant la macro précédente, et en changeant seulement les deux derniers objets initiaux : M(t0+h) et V(t0+h) pour le point suivant, etc ... ce qui permet de réaliser une approximation de la conique par une méthode d'ordre 2 en construisant la Cabri-conique passant par les 5 points. On notera que le dernier point V(t0+4h) produit par la macro ne sert pas. Dans l'illustration ci-contre on a placé M(t0) et V(t0) pour que la conique soit une ellipse, mais à priori, cela peut aussi être une hyperbole (voir illustration ci-dessous). La figure SolEuler.fig

Illustration avec une composante v(t0) différente

 

Convergence de la méthode

On peut s'interroger sur la validité expérimentale de notre construction: quelle convergence? sa rapidité? queele stabilité pour la courbe ?... On pourra se contenter de faire varier h pour en avoir une visualisation du résultat. On voit qu'à partir de h = 1/32, avec ces données initiales, les coniques se confondent sur une conique solution du problème. La figure Converg.fig

Remarque : d'après la première loi de Képler, O est un foyer de la conique. On peut aussi construire les foyers des coniques et voir leur convergence vers un point. La macro Foyers d'une conique pour les ajouter à la figure de départ. La figure ConvFoy.fig ci contre pour sa manipulation en 1/h.

Il existe une méthode de construction exacte de la courbe dans le cas de deux corps: nous allons dans le paragraphe suivant présenter cette méthode pour pouvoir la comparer à la méthode d'Euler.

Sur le centre de courbure

La " cinématique du point " nous apprend que la composante normale de l'accélération du point M a pour norme V2/Pm où Pm est le rayon de courbure de la trajectoire en M. Or les conditions initiales nous donne la position M0 de M par rapport à O à l'instant t0 - vecteur position r(to) = OM0 - et la vitesse de M v(t0) représenté par un point V0 tel que v(t0)=M0V0 L'accélération a est fournie par la loi de Newton: c'est un vecteur dirigé de M0 vers O et de norme m/r2. Construisons ce vecteur a. (L'illustration ci-contre est proposée avec a(t0) déjà construit à partir de la masse m et de l'unité. Elle détaille la construction de Pm à partir de M0.

La composante tangentielle a_T du vecteur a est le vecteur projeté de a sur la droite (M₀V₀).
On sait alors construire la distance P_m=V₀²/a_N et si l'on note C le centre de courbure en M, on sait que le vecteur MC a même direction et sens que le vecteur a_N (composante normale du vecteur a). On peut donc construire le point V₀²/a_N puis le point C en le ramenant sur la demi-droite [M₀a_N).

On observera (éventuellement) la construction algébrique de la multiplication et de la division.

La figure CerclOs1.fig ci dessus

La macro CCOsPlan.mac d'objets initiaux m (2 pts gauche, droite), l'unité (idem), les points O, M₀ et V₀ et qui renvoie le centre C du cercle osculateur.

Construction de la conique exacte

Résumons tout ce que nous avons trouvé. Nous avons comme informations à l'instant t₀ la position de M, le point V, le point O qui est un des foyers de la conique et le centre de courbure C en M. Ces informations suffisent pour construire la conique en utilisant la propriété suivante :

F et F' étant les foyers d'une conique passant par M, et C le centre de courbure de M. Notons P et P' les intersections des droites (MF) et (MF') avec le cercle de diamètre [MC]. Alors (MC) est la médiatrice du segment [PP']. Et de plus le point I, milieu de [PP'], est un point de l'axe focal. Pour faire la figure, Charger les macros du site : Coniques par F, F', M et Cercle osculateur à une conique ou Lancer la figure PropCOsc.fig (cas ellipse)

On va donc construire le second foyer de la conique (quand il existe) et construire la figure par foyer et cercle directeur associé. Cette démarche s'appuie sur le fait qu'en prenant des points de base, la probabilité de rencontrer le cas parabole n'est pas tout à fait nulle, mais si faible ...

Charger la macro Conique par Foyer et Cercle directeur pour terminer la figure déja présentée à cette page.

Connaissant O (le foyer F), M et C (de la macro précédente), cette propriété permet de déterminer l'autre foyer O', et donc la conique en utilisant une macro sur les cercles directeurs.

La droite (MO) coupe le cercle de diamètre [MC] en P. La perpendiculaire à (MC) passant passant par P coupe (MC) en I.

La droite (OI) est alors l'axe focal de la conique. L'un des foyers étant O, l'autre O' s'obtient comme intersection de la droite (MP') où P' est le symétrique de P par rapport à la droite (MC), et de l'axe focal (OI). On peut alors construire le cercle directeur de la conique associé à O, c'est-à-dire le cercle de centre O' et passant par le symétrique K de O par rapport à la droite (MV) puisque M est un point de la conique et que (MV) est la tangente à la conique en M.On termine en appliquant la macro ci-dessus. La figure SolExact.fig ci-contre.

La macro Mouvement des planètes (fichier SolExact.mac) qui, à partir des objets initiaux la masse m, l'unité, O, M et V, renvoie la conique mouvement de M (de masse 1) autour du soleil de masse m quand elle est animée d'un vitesse intiale de vecteur MV.

Comparaison de la méthode d'Euler et de la solution

La figure Compare.fig précédente pour faire varier h et les paramètres de masse de distance et de vitesse initiale. On voit que quand h tend vers 0, l'approximation d'Euler converge vers la solution (heureusement).

Nature de la conique obtenue

Les calculs mis en évidence par Newton donnent les résultats suivants :

Traçons alors un cercle de centre O et de rayon 2m/V₀², avec V₀ = MV, on obtient :

La figure Finale.fig ci-dessus dans laquelle il faudra redéfinir O sur le cercle pour avoir le cas de la parabole.

Contact avec l'auteur : Daniel Courounadin

Son site (activités mathématiques interactives - en Java et JavaScript - pour le collège)

 

Retour "Coniques"

Menu général

 

 

Note à propos de la méthode d'Euler d'ordre 2

Dans la thèse récente (1996) de Dominique Tournès, intitulée "L'intégration approchée des équations différentielles (1671 - 1914)", il est précisé que la méthode utilisée ici, sur ses conseils, a servi à Euler pour calculer la trajectoire d'une comète en 1774 :

"Le passage de la comète de Halley, en 1759, avait fait naître des craintes à propos du danger que pourrait présenter une comète s'approchant très près de la Terre. Y avait-il un risque de collision ? L'orbite terrestre pouvait-elle être modifiée de façon importante ? La comète pouvait-elle être satellisée et devenir une seconde lune ?

La comète de Lexell, en 1770, relança ces interrogations. Les observations montraient qu'elle semblait décrire une orbite elliptique avec une période de révolution d'environ 5 ans et demi, alors qu'on ne l'avait jamais vue auparavant ! Une étude plus fine permit de découvrir qu'elle avait dû passer très près de Jupiter ; on fit alors l'hypothèse que la planète géante avait fortement modifié sa trajectoire, à tel point que, d'invisible lors de ces précédents passages, elle était devenue visible en 1770.

C'est dans ce contexte qu'Euler réalise, en 1774, une étude sur les consèquences du passage d'une comète à proximité de la Terre. (...) Euler emploie la méthode décrite dans le second volume des Institutiones calculi integralis."

Le texte reprend ensuite et commente les calculs d'Euler (pages 178 à 184), avec des conclusions, quant à ladite comète, que l'on imagine.

Pour information, la thèse de Dominique Tournès (formateur à l'IUFM de La Réunion) est désormais disponible aux éditions du Septentrion (240 F) :

Presses Universitaires du Septentrion
rue du Barreau - BP 199
59654 Villeneuve d'Ascq Cedex

Retour