Cabri-conique définie par
foyer et cercle directeur

1 - Macro de base - Premières propriétés

 [2 - Cercle principal et tangentes] [3 - Applications immédiates]
[Retour Présentation "Bifocale"] [Retour Coniques] [Exemples d'utilisations]

 

La définition bifocale des coniques s'entend généralement par la donnée de deux foyers F et F' et d'une distance 2a telle que, selon qu'il s'agisse d'une ellipse ou d'une hyperbole, la conique soit l'ensemble des points M vérifiant :

Ellipse

MF + MF' = 2a

Hyperbole

|MF - MF'| = 2a

Cette définition est équivalente à la donnée d'un des deux foyers F' et du cercle de centre l'autre foyer F et de rayon 2a. Ce cercle est appelé cercle directeur associé au foyer F'. Dans ces pages nous favoriserons cette approche. La construction d'un point A de la conique à partir d'un point U du cercle est décrite ci-dessous.

Macro d'une conique bifocale

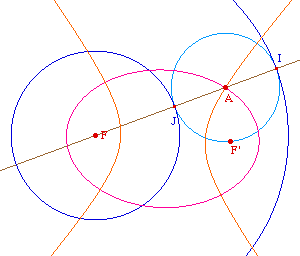
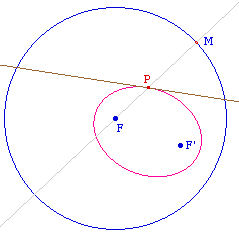
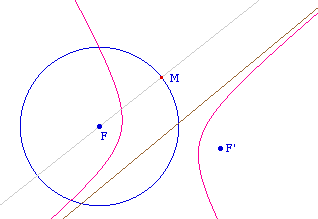
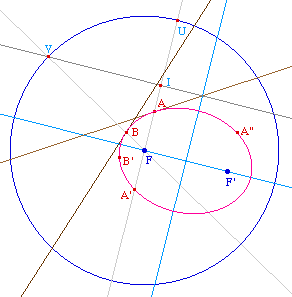
Etant donnés un cercle C de centre F et un point F', pour construire la Cabri-conique de foyer F' et de cercle directeur associé C, il suffit d'en construire deux points A et B. On complète ensuite en utilisant les deux axes de symétrie connus que sont (FF') et la médiatrice de F et F', ce qui donne les points A', B' et A".

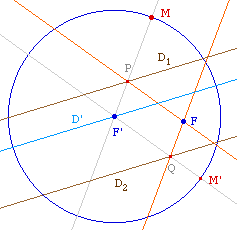
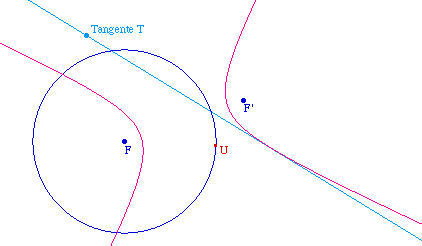
Pour construire les points A et B, on construit deux points U et V du cercle directeur C. Ici, ils sont pris à partir de la perpendiculaire en F à l'axe focal et de la médiatrice de [FU].

U étant construit, on rappelle que le point A de la conique issu de U est l'intersection de la médiatrice de [F'U] et de la droite (FU).

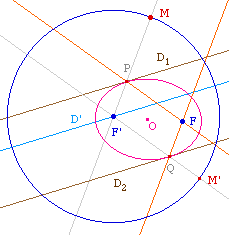
Remarque : si on prend le segment [FU] au lieu de la droite (FU), on s'impose à ne construire que des ellipses, ce qui peut être une macro logique intéressante dans certains cas.

CnkFC1.fig.

La macro Conique par foyer et cercle directeur (fichier CnkFC1.mac) d'objets initiaux le foyer et le cercle directeur associé. Cette macro est utilisée dans tout le reste de la page, et dans les pages suivantes.

Exemple d'utilisation immédiate

Soient trois points F, F' et A. On s'intéresse aux coniques de foyers F et F', et passant par A. Le cercle de centre A passant par F' coupe la droite (FA) en I et J.

Le cercle de centre F passant par I est cercle directeur associé à F de l'unique ellipse solution, alors que le cercle de centre F passant par J est cercle directeur associé à F de l'unique hyperbole solution, chacune des deux coniques étant construite par la macro précédente.

Remarque : plus précisément I est défini comme le point tel que les vecteurs FA et FI soient R+-colinéaires, J étant l'autre point.Alors l'inégalité triangulaire assure que F' est à l'intérieur du cercle de centre F passant par I (ellipse) alors qu'il n'est pas à l'intérieur de celui de centre F passant par J (hyperbole).

On peut en déduire plusieurs macros (non utilisées dans cette page) :

Macro Coniques de foyers F, F', passant par A (Fichier Cnk2F1pt.mac)

Macro Ellipse de foyers F, F', passant par A (Fichier Ell2F1pt.mac)

Macro Hyperbole de foyers F, F', passant par A (Fichier Hyp2F1pt.mac)

 

Centre des coniques bifocales

Nous nous proposons ici de montrer géométriquement l'existence du centre d'une conique définie par foyer et cercle directeur.

On considère un cercle de centre F', un point F quelconque différent de F'. Soit M un point du cercle. On note :

D1 la médiatrice de [FM],
D' la parallèle à D1 passant par F'
M' le sym. de M par rapport à D'
D2 la médiatrice de [FM']
P l'intersection de D1 et (F'M)
Q l'intersection de D2 et (F'M').

(PF) étant symétrique de (PM) par rapport à D1, (F'Q) de (F'M) par rapport à D', et D' étant parallèle à D1, les droites (F'Q) et (PF) sont parallèles. De même on a (F'P) parallèle à (QF).

Donc F'QFP est un parallèlogramme.

Or la construction précédente n'est rien d'autre que celle de deux points de la conique de foyer F et de cercle directeur associé le cercle de centre F'.

On vient donc de montrer que pour tout point M du cercle, on sait construire un point Q tel que si P est le point de la conique associé à M, Q est un point de la conique symétrique de P par rapport au milieu de [FF'].

Les coniques bifocales ont donc un centre de symétrie qui est le milieu des foyers.

CnkCntr1.fig.

On observera éventuellement sur la figure précédente l'argument dans le cas de l'hyperbole :

Tangente à une conique bifocale

Dans la construction précédente, on sait de plus que la médiatrice du segment [MF'] est la tangente à la conique en le point associé P, intersection de cette droite avec la droite (FM).

Preuve

Pour le montrer dans le cas de l'ellipse, il suffit de savoir que que si une droite coupe une ellipse en un seul point, alors c'est une tangente, cette propriété étant issue soit des constructions d'intersection droite/ellipse, soit encore de la transformation du cercle en ellipse par affinité.

Soit alors un point N de la médiatrice de [F'N]. Par inégalité triangulaire dans FNM, ce point N ne peut vérifier FN + FN' = 2a donc N ne peut appartenir à l'ellipse.

Pour le cas de l'hyperbole, il faut savoir qu'une droite ne coupe une hyperbole en un point que si elle est tangente ou parallèle à une asymptote (voir les propriétés spécifiques des coniques dans un autre item).

Soit alors N un autre point que P de la médiatrice de [F'N], pour la branche donnée. On ne peut avoir cette fois NF - NF' = 2a car alors on aurait, comme ci-dessus NF - NM = 2a = MF, donc les points F, M et N alignés de qui n'est pas.

Ainsi, la médiatrice de [F'M] n'a qu'un point commun avec l'hyperbole .../...

.../...

Or de plus, l'existence du point P prouve que les droites (FM) et la médiatrice de [F'M] ne sont pas parallèles. Or ces droites sont parallèles si et seulement si M est le point de contact du cerle avec une tangente issue de F'. On est dans le cas où (FM) est une direction asymptotique.

Donc, si P existe, la médiatrice de [F'M] n'est pas parallèle à une asymptote. Si cette droite n'a qu'un point commun avec l'hyperbole, c'est bien qu'elle est tangente à la conique.

Exemple d'utilisation immédiate

On peut en déduire une construction d'une conique dont on connaît deux foyers et une tangente. Il suffit de prendre le symétrique d'un foyer (ci-dessus F') par rapport à cette tangente (point U). Alors le cercle de centre l'autre foyer passant par ce point est le cercle directeur associé au premier foyer.

La figure Cnk2F1Tg.fig précédente.

La macro Conique par 2 foyers et 1 tangente (fichier Cnk2F1Tg.mac) d'objets initiaux les deux foyers et la tangente.

 

 [2 - Cercle principal et tangentes] [3 - Applications immédiates]
[Retour Présentation "Bifocale"] [Retour Coniques] [Exemples d'utilisations]

 

Menu général