5.B - Troncature opaque du cube par les arêtes

 [Retour à la page 5]

 [1 - Ombre d'une échelle] [2 - Tiroir d'une commode] [3 - Urbicande]
[4 - Troncature opaque du cube par les sommets]

La figure de départ

 

Dans cette fiche, la figure utilisée est celle déjà réalisée dans la rubrique Espace : la troncature se fait sur une demi-arête. Comme pour les autres traitements de l'opacité, par défaut, les arêtes sont invisibles, donc en pointillé. Les arêtes de la face du haut sont visibles.   La figure TrAOpk01.fig de départ.

Comme dans les autres troncatures, on choisit à nouveau de privilégier la gestion des faces visibles. Il y a ici 4 type de faces, trois types de faces hexagonales, et un type de faces carrées.

La seule difficulté est dans le maintient des critères de visibilité tout au long de la troncature puisque les faces changent de nombre d'arêtes, sans changer de branche logique comme pour la troncature par les sommets. Par exemple une construction sur la base d'une droite passant par deux points disparaîtra quand les deux points seront confondus.

Il en résulte des constructions parfois moins élémentaires que dans les autres gestions de l'opacité, soit nécessitant des correctifs pour certains cas particuliers.

Si vous souhaitez faire la figure en ligne, vous aurez besoin de :

Charger la macro Ping-Pong

Les faces hexagonales supérieures

Dès ce premier type, nous rencontrons la nécessité d'un traitement particulier. En effet, une méthode classique, comme dans les autres figures de troncature, basé sur le fait qu'une figure est visible si elle est d'un côté d'une arête, si elle est applicable, perd de sa pertinence quand on tronque de telle façon que cette arête n'existe plus. Par exemple ci--dessous la face est visible si et seulement si elle est à droite le la droite (ab), soit dans l'autre demi-plan que z délimité par (ab). Mais il faut procéder autrement, car quand la troncature n'a pas commencé, la droite (ab) n'existe pas.

On va en profiter pour proposer un exemple de macro-construction de visibilité intrinsèque, ne faisant référence qu'au solide en rotation sans utiliser des points du repère comme on le fait dans les autres constructions. Dans cette figure, la face est visible si u existe, comme intersection d'une droite et d'un segment. Mais pour que u existe dans tous les cas, même en troncature maximale, on ne peut pas se baser sur la droite (af) qui alors n'existe plus. La droite est donc la parallèle à [be] passant par a. La construction se termine alors classiquement avec des points conditionnés à l'existence de u (par Ping-Pong) sous a, c, et e. La figure TrAOpk02.fig pour tester sa résistance aux cas limites.

On observera alors que u existe bien dans ces cas, comme illustré ci-contre. On peut aussi choisir de Charger la macro FcHexSup.mac (Face Hexagonale Supérieure) pour l'appliquer à la figure initiale, d'objets initiaux : a, b, c, d, e, f, et h le sommet de l'autre arête issue de a. Ou encore ... Charger la figure TrAOpk03.fig comprenant l'application de cette première macro.

Les faces hexagonales inférieures

 

On remarque que la même macro Face Hexagonale Supérieure peut aussi s'appliquer, en choissant pour le point h le point correspondant à a sur la face opposée. Bien-sûr cette macro ne construit pas l'arête supérieure de la face, mais ce n'est pas un problème car la face carrée correspondante a une visibilité plus grande de la face hexagonale inférieure, comme on peut déjà le voir sur l'illustration ci-contre. La figure TrAOpk04.fig comprenant l'application de cette macro aux faces inférieures. On peut remarquer que la figure est correcte dans la troncature maximale, mais qu'un problème subsiste dans l'application de la macro au départ : le point u existant toujours dans ce cas, la macro renvoie un segment toujours existant. Ainsi, au début de la troncature, les 4 arêtes du bas sont visibles, il faudra corriger ce point.

Les faces carrées

 

Puisque l'arête supérieure des faces précédentes n'est pas construite, on s'intéresse à la construction des faces carrées. On peut classiquement appliquer une macro Face Carrée Visible. Cette macro, construite dans un autre contexte, utilise la droite (ab), mais comme la face carrée n'existe pas quand la droite n'existe pas, cela ne pose pas de problème sur le plan de la construction des arêtes. La macro Face Carrée Visible d'objets initiaux a, b, c, d et z.

Les faces hexagonales verticales

 

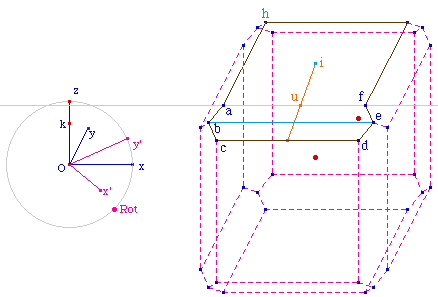
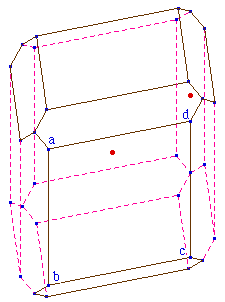
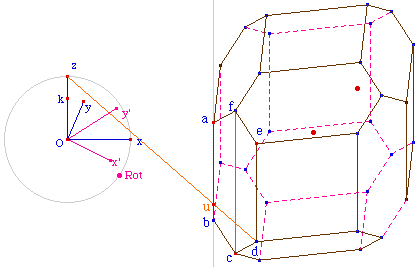
La construction est encore un classique du genre. Ici, pour que l'arête [bc] existe même si a et b sont confondus - elle est alors une arête de la face losange - il faut que la construction existe toujours. Ainsi, au lieu de tracer la droite (ab), on construit la parallèle à [cf] passant par a. Le reste se fait comme d'habitude, on construit sous a, c, e des points conditionnés à l'existence de u. 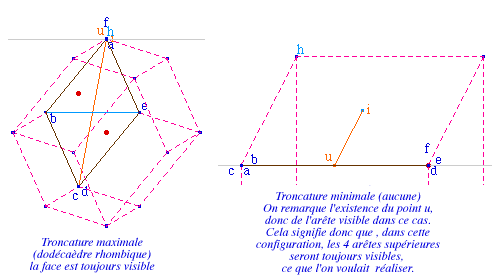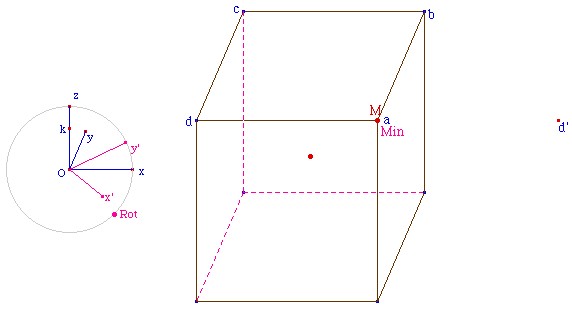On remarquera que la construction de toutes les arêtes sont nécessaires, car pour certains angles de la perspective cavalières, les arêtes [af] et [fe] sont nettement détachées et ont effectivement besoin d'être rendues visibles. La figure TrAOpk05.fig de travail pour observer le comportement de la construction. 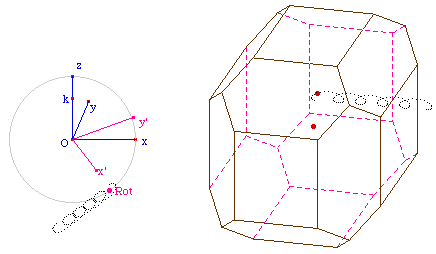La macro FcHexVer.mac d'objets initiaux a, b, c, d, e, f et z. 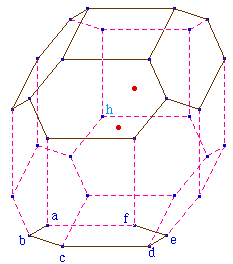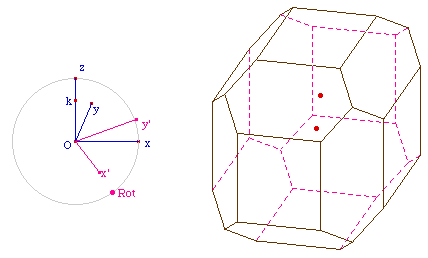La figure TrAOpk06.fig comprenant l'application de cette macro aux faces hexagonales verticales, ce qui "achève" (momentanément) la construction.

Pour s'apercevoir que la construction n'est pas tout à fait terminée, on peut observer le comportement de la figure précédente, dans la configuration où la troncature n'a pas commencé. TrAOpk07.fig , figure précédente nettoyée de tous ses points de construction. On observe alors que cette figure est correcte en tous points, sauf quand M est au sommet du cube : le point u (de la macro des faces hexagonales du bas (la même que celles du haut) existe quand M est au sommet : ce comportement est trés intéressant pour la face du haut, cela rend les 4 arêtes visibles, mais ne n'est plus pour celles du bas, car alors, quand M est au sommet, toutes les faces deviennent visibles : il y en a 3 de trop. Il faut donc effectuer ...

 

Une modification cosmétique

Nous avons beaucoup utiliser dans toutes ces constructions que c'est le dernier segment construit qui est affiché. Il nous faut donc construire un nouveau segment pour les faces non visibles, quand M est au sommet a comme ci-dessous.

Soit d' le symétrique de d par rapport à a. M est en a si et seulement si M appartient au segment [ad'], ce qui se teste par l'existence d'un point Min issue de la macro Intérieur segment.

A partir de ce point, on construit, sur celui d'origine un nouveau cube qui n'existe qui si le point Min existe (en utilisant le centre de symétrie). On construit alors 12 nouvelles arêtes de couleur "face invisible", sauf pour les 4 de la face de dessus.

Puis il suffit d'appliquer 4 fois la macro Face Carrée déjà proposée un peu plus haut. On peut même enlever les arêtes supérieures que la macro construit.

Cette fois ci, la figure est bien terminée.

Charger la figure TrAOpkF.fig, réellement finale.

 [Retour à la page 5]

 [1 - Ombre d'une échelle] [2 - Tiroir d'une commode] [3 - Urbicande]
[4 - Troncature opaque du cube par les sommets]

Menu général