4.B - Troncature opaque du cube par les sommets
Détail de la première branche

[Retour à la page 4]  [Page 4.C]

 [1 - Ombre d'une échelle] [2 - Tiroir d'une commode] [3 - Urbicande]
[5 - Troncature opaque du cube par les arêtes]

La figure de départ

Deux attitudes sont possibles pour le traitement de l'opacité des arêtes : soit travailler sur les arêtes individuellement, soit raisonner sur les faces. La seconde méthode est plus facile, mais amène en contre partie à construire souvent deux segments par arête, puisque chaque arête appartient à deux faces. C'est néanmoins l'attitude adoptée dans cette fiche, car elle est géométriquement plus lisible, et plus rapide à mettre en oeuvre.

On notera également que la figure chargée contient déjà, pour l'avoir utilisée, la macro Ping-Pong, omniprésente dans les constructions ci-dessous.

Les faces triangulaires supérieures

On distinguera en effet les faces triangulaires du haut, pour lesquelles une arête est toujours visible de celles du bas, où il faut construire les trois côtés : la démarche peut être optimisée dans le cas des faces supérieures.

Leur traitement reprend l'idée vue dans les faces opaques d'un cube : une face triangulaire supérieure est visible si sa partie gauche est à gauche de son sommet le plus à droite. D'où la construction ci-dessus, reprise de celle du cube : la face abc est visible si le segment [zc] coupe la droite (ab). La face visible est alors matérialisée par la construction de deux segments construits à partir d'un point sous b, conditionné à l'existence de u. On peut faire la figure et la transformer en macro ou directement La macro FaceTR.mac (Face TR Sup Visible) pour l'appliquer à la figure initiale.   La figure TrSOpk02.fig ayant ses faces triangulaires supérieures traitées.

Les faces triangulaires inférieures

 

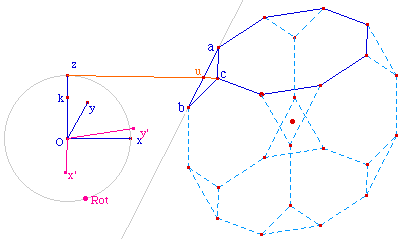
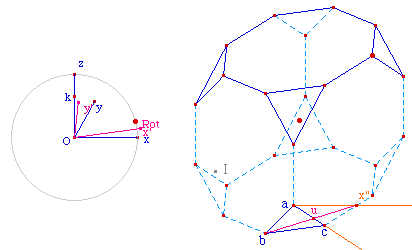
On observe ici que la face abc (illustration ci-dessus) est visible si et seulement si l'angle bac est positif (dans un repère trigonométrique du plan usuel). Il faut donc chercher une construction simple de Cabri qui rende compte de cette orientation de cet angle. Nous proposons la suivante, qui n'est pas nécessairement la meilleure : Soit x" le translaté de x du vecteur Oc (pour avoir une demi droite horizontale issue de c). Ici on a utilisé le milieu I de x et a, mais on aurait pu utilier un vecteur. Alors l'arête est visible si et seulement si le segment [bx"] coupe la demie-droite [ac). Soit u ce point, on termine par trois segments conditionnés par l'existence de u. La figure TrSOpk03.fig de travail pour observer l'argument décrivant la visibilité de la face, la macro FaceTRBs.mac (Face TR Inf Visible) pour l'appliquer à la figure précédente (ordre des points a, b, c, O et x), ou encore charger la figure TrSOpk04.fig ayant ses faces triangulaires inférieures traitées.

Les arêtes des faces latérales octogonales

 

Leur traitement est exactement comme celui des faces du cube : une face latérale octogonale est visible si sa partie gauche est à gauche de sa partie droite. D'où la construction ci-dessus, reprise de celle du cube : une face est visible si un segment partant de z allant sur un point de l'arête droite verticale coupe la droite passant par l'arête gauche verticale. La face visible est alors construite à partir de trois points conditionnés par cette intersection sur l'octogone. On peut faire la figure et la transformer en macro ou directement Charger la macro FaceOcto.mac (Face Octogonale Visible) pour l'appliquer à la figure précédente, ou encore, lancer la figure TrSOpk05.fig ayant ses faces latérales traitées, ce qui termine cette première branche.

[Retour à la page 4]  [Page 4.C]

 [1 - Ombre d'une échelle] [2 - Tiroir d'une commode] [3 - Urbicande]
[5 - Troncature opaque du cube par les arêtes]

Menu général