Le mouvement tractionnel en géométrie

2 - Tractrice et autres tractoires

2.2.b. Tractoire à base un lieu dans Cabri

2.2.a. Tractoire à base circulaire

En dehors des droites, des cercles et des coniques, les autres courbes que l'on peut tracer dans Cabri, c'est-à-dire les lieux de points, souffrent de restrictions qui ne permettent pas de reconduire telles quelles les constructions des paragraphes précédents. En effet, Cabri ne sachant pas trouver l'intersection d'un lieu et d'une droite, on ne peut pas réaliser directement un partage en 16 d'un arc de courbe. Je vais donc expliquer comment il convient de s'adapter à cette nouvelle situation.

Principe d'une tractoire à base un lieu de Cabri - Exemple de la sinusoïde

Considérons tout d'abord la courbe représentative d'une fonction f, tracée dans un repère. On suppose qu'on a préparé une macro qui à un point générique de l'axe des abscisses, d'abscisse x, associe le point de coordonnées (x, f(x)). Si la fonction f est constructible à la règle et au compas, cette macro est une construction à la règle et au compas (même si, en pratique, on s'autorise à utiliser la calculatrice pour aller plus vite) ; dans le cas contraire, par exemple pour une fonction transcendante faisant intervenir les logarithmes ou les lignes trigonométriques, la macro est nécessairement une construction approchée utilisant les approximations fournies par la calculatrice.

TracSin1.fig ou la macro TractS16.mac

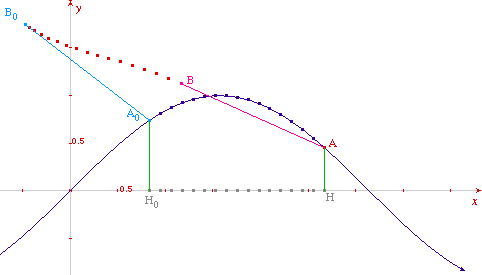
Pour fixer les idées, j'appuierai la suite de mon propos sur l'exemple de la fonction sinus. Prenons un point quelconque A₀ sur la courbe et un point quelconque B₀ n'importe où : le segment [A₀B₀] représente, comme d'habitude, la position initiale du fil. Prenons un autre point quelconque A sur la courbe. Le partage en 16 de l'arc A₀A se fait via le partage en 16 de sa projection orthogonale [H₀H] sur l'axe des abscisses et via la macro évoquée ci-dessus qui permet de construire les points correspondants de la courbe. Il ne reste plus qu'à appliquer 16 fois 16 fois la macro TractInst.mac pour obtenir la position finale AB du fil.

En enregistrant une macro qui, aux axes et aux points A₀, B₀ et A, associe le point final B (et les macros analogues pour des partages en 32 et 64 parties), on dispose de l'outil adéquat pour explorer les tractoires d'une courbe représentative de fonction.

En demandant, selon une procédure maintenant bien établie, le lieu de l'extrémité B lorsque l'extrémité A parcourt la courbe, on obtient une tractoire ayant pour base la courbe donnée, ici la sinusoïde. Si on déplace ensuite le point A de la gauche vers la droite à partir de A₀, on simule le mouvement tractionnel d'un fil posé sur un plan horizontal et que l'on tire le long d'une sinusoïde.

TracSin2.fig

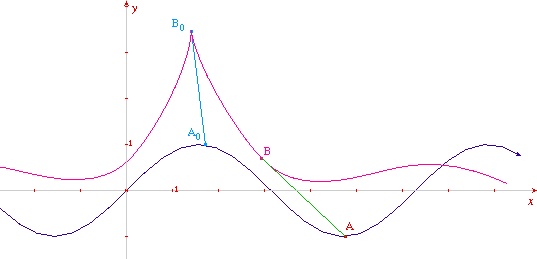
Note à propos des macros : pour changer rapidement de fonction sans tout refaire, il est plus simple d'éditer les macros dans un éditeur de texte et remplacer " sin(a) " par " f(a) ". Dans une figure comme la première, la fonction f est utilisée une seule fois car elle est en macro interne à la figure. Par contre dans une figure comme la seconde, elle est utilisée 16 fois (ou 64) car Cabri ne gère pas des macros internes aux macros et reconvertit tout en texte unique. Il faut donc faire un "remplacer partout".

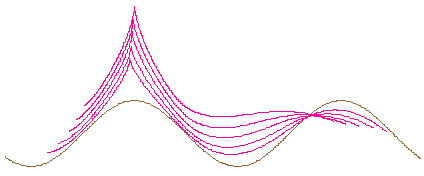
On peut faire de belles figures pour s'amuser, par exemple en traçant simultanément plusieurs tractoires avec des fils de même direction initiale mais de longueurs différentes.

 

Problème inverse

Les lecteurs rapidement parvenus à ce point de l'exposé doivent se dire : tout ça, c'est bien beau, mais ce ne sont que des petits dessins ; non seulement ça ne sert à rien, mais en plus il n'y a pas de démonstrations et, le comble, c'est qu'on ne sait même pas si on fait de la géométrie ou de l'analyse !

Pour relever le niveau, il serait temps d'écrire quelques formules. Mais où en trouver ? Heureusement qu'un vieux réflexe mathématique fait surgir en moi une question salvatrice : quid du problème inverse ? Jusqu'ici, on s'est donné une courbe de base, déjà tracée sur le papier, et on a construit une tractoire de cette courbe. Inversement, une courbe étant donnée, existe-t-il une courbe de base dont la courbe donnée soit une tractoire ?

Soit donc une courbe donnée, d'équation y = f(x). Considérons un segment de tangente de longueur a, d'origine le point B de coordonnées (x, f(x)) et d'extrémité le point A de coordonnées (x + u, f(x) + v). On supposera u > 0 pour garder l'idée qu'on déplace un fil de la gauche vers la droite. Les nombres u et v sont caractérisés par : le fil AB est de longueur a, c'est-à-dire a = u2 + v2 ; le fil AB est tangent à la courbe, c'est-à-dire v = f '(x).u

On en déduit sans difficulté que :

Finalement, lorsque le point B décrit la courbe donnée, le point A décrit la courbe paramétrée définie par :

Et donc, inversement, la courbe donnée est une tractoire de cette courbe paramétrée !

Prenons un exemple simple, celui de la parabole d'équation y = f(x) = x2. Puisque f '(x) = 2x, les formules précédentes montrent que cette parabole est une tractoire de la courbe paramétrée dont les relations sont données ci-contre (avec le paramètre t pour éviter des confusions) :

Il n'y a plus qu'à se lancer dans la construction de cette courbe paramétrée (c'est possible à la règle et au compas) et adapter ce qui a été fait plus haut (dans les figures ci-dessous, j'ai pris a = 1 pour fixer les idées). La principale différence est que le point courant A de la courbe ne se manipule plus directement à la souris, mais indirectement par l'intermédiaire de son paramètre t , représenté par un point générique de l'axe des abscisses. Concrètement, on peut imaginer un appareil mécanique qui déplace l'extrémité A du fil : l'opérateur ne tire plus lui-même, à la main, sur l'extrémité A du fil, mais déplace un curseur t sur la console de l'appareil.

CParam1.fig et la macro associée TracCP16.mac

À part ça, tout se déroule de manière analogue. Le partage en 16 (ou en 64) de l'arc de courbe A₀A s'obtient par l'intermédiaire du partage du segment [t₀t]. Une fois les macros mises au point, il n'y a plus qu'à tracer une tractoire de la courbe paramétrée.

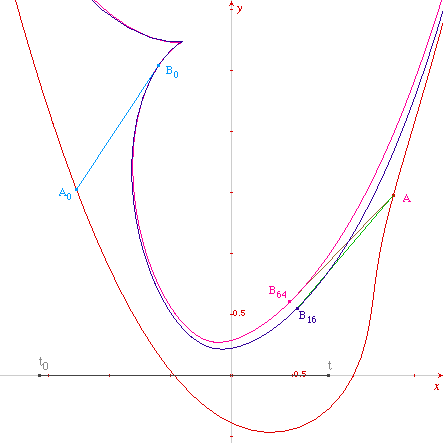
CParam2.fig (comparaison des précision avec 16 et 64 pas)

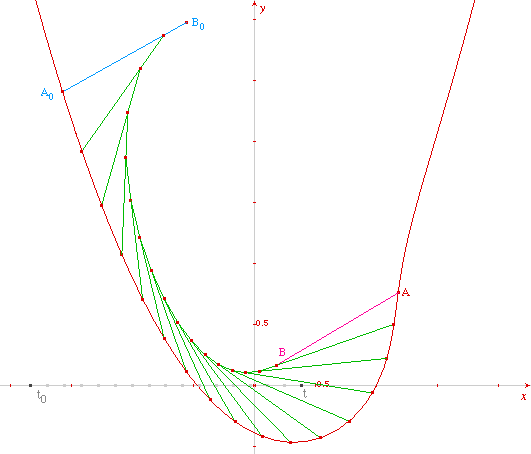
Ceci étant dit, fait et médité, tout est prêt pour une construction peu banale de la parabole d'équation. Il suffit de choisir la condition initiale, c'est-à-dire la position de départ A₀B₀ du fil, de sorte que ce soit une tangente à la parabole. Le plus simple est de mettre le fil le long de l'axe des abscisses, avec B₀ à l'origine (puisqu'on sait que l'axe des abscisses est tangent à la parabole à l'origine).

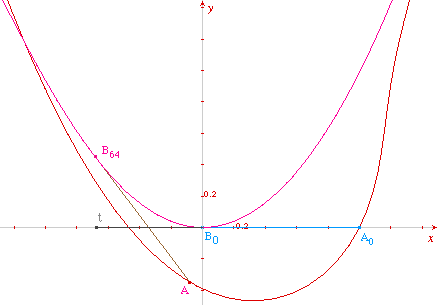
En rose, la parabole obtenue comme tractoire de la courbe paramétrée rouge

On construit ainsi la parabole en tant que tractoire ayant pour base une courbe constructible à la règle et au compas. On peut vérifier sur la dernière figure que le tracé est remarquablement précis, du moins dans un voisinage de l'origine (de façon générale, il est clair que les constructions de ce dossier sont excellentes autour de la position initiale, mais que la précision se dégrade au fur et à mesure qu'on s'en éloigne).

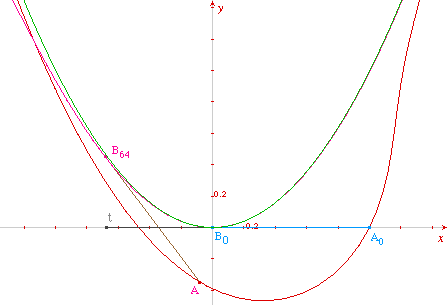
CParam3.fig (en vert la parabole exacte, tractoire de la courbe paramétrée rouge)

Là, les grincheux vont crier au scandale : quoi, tout ça pour construire une parabole ! Le site abraCAdaBRI, jadis réputé pour son sérieux, autrefois loué pour la simplicité et l'élégance de ses constructions, n'est vraiment plus ce qu'il était…

Plus fondamentalement, cet exercice de style met en évidence une limitation pratique de la théorie des tractoires telle qu'elle a été développée jusqu'ici. La contrainte d'utiliser un fil de longueur constante est vraiment désagréable : elle introduit dans les calculs une racine carrée dont on n'arrive pas à se défaire et elle conduit parfois à supposer connues des courbes plus compliquées que celles que l'on cherche à construire !

Pour progresser, il ne reste qu'une issue : il faut accepter que la longueur du fil devienne variable. Après tout, rien n'empêche d'imaginer qu'au cours du temps, dans notre appareil mécanique (réel ou virtuel), le fil se dévide d'une bobine selon une certaine loi…

C'est ce que nous allons explorer dans la partie 2.3.

 2.2.a. Tractoire à base circulaire | Haut

Menu général