[Application aux équations différentielles] [Tractrice et pseudo-sphère] [Retour "Courbes et équations"]
En 1670, Leibniz rencontre à Paris le médecin Claude Perrault : ce dernier sort sa montre, la pose sur une table, déplace l'extrémité de la chaîne le long du bord rectiligne de la table et demande à Leibniz quelle est la courbe décrite par la montre.
Leibniz, puis Newton, Huygens, les frères Bernoulli, L'Hôpital et bien d'autres s'emparent avec enthousiasme de ce problème qui va fasciner les mathématiciens jusqu'au milieu du XVIIIe siècle. Leibniz nomme la nouvelle courbe tractrix, Huygens préfère l'appeler tractoria, aujourd'hui on parle de tractrice.
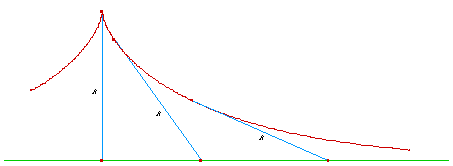
La tractrice est définie par la propriété que le segment de tangente situé entre la courbe et l'axe des abscisses demeure constant, puisque ce segment représente la chaîne - ou le fil - de longueur constante dont une extrémité est déplacée le long de l'axe (en raison du frottement, l'objet situé à l'autre extrémité suit à chaque instant la direction dans laquelle il est tiré par le fil).

L'équation différentielle de la partie droite de la courbe est :
En intégrant cette équation avec la condition initiale y(0) = a, on obtient
Si l'on sait construire la courbe logarithmique, c'est-à-dire si l'on sait réaliser la quadrature de l'hyperbole, alors on peut construire la tractrice. Mais, à la fin du XVIIe siècle, les logarithmes, encore peu familiers, n'inspirent guère confiance aux géomètres. Et comment pourrait-on se contenter, en géométrie, d'une courbe simplement tracée par points à partir de valeurs approchées lues dans des tables ?
C'est là que la tractrice se met à devenir intéressante, lorsqu'on examine le problème à l'envers. Si l'on sait construire la tractrice, alors on peut réaliser de façon exacte la quadrature de l'hyperbole, et donc aborder de manière plus satisfaisante tous les problèmes qui font intervenir des logarithmes. Or, la tractrice, engendrée par le mouvement continu d'un fil que l'on tire, ne diffère finalement en rien de la droite et du cercle, eux-mêmes engendrés par un mouvement continu lors de l'utilisation d'une règle ou d'un compas.
Voilà donc ce qui a tant intéressé nos géomètres : ils pressentaient qu'en ajoutant la mouvement tractionnel aux mouvements rectiligne et circulaire qui sont depuis toujours aux fondements de la géométrie, ils pourraient traiter de manière exacte une nouvelle classe très étendue de problèmes.
Diverses tentatives furent faites pour fabriquer des instruments permettant d'exploiter concrètement le mouvement tractionnel :
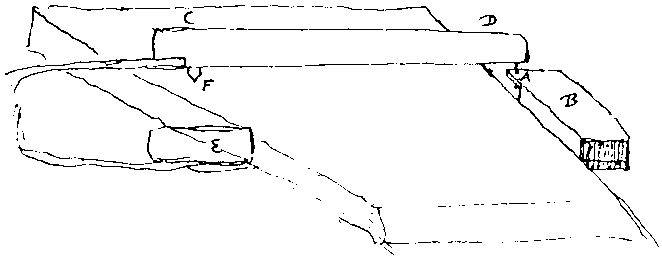
Huygens - Schéma d'un appareil pour tracer la tractrice
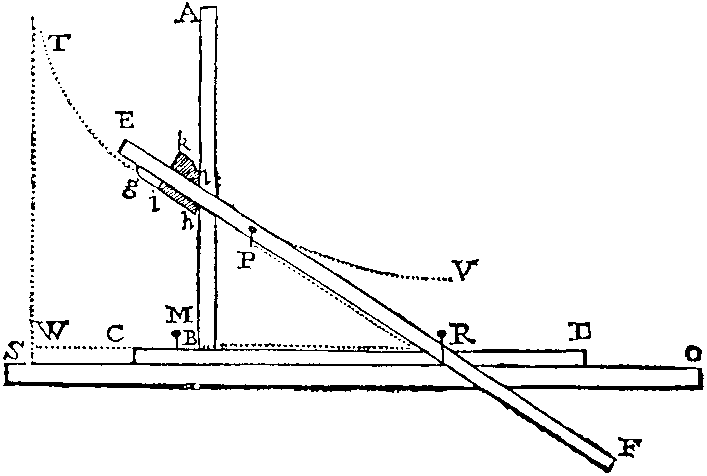
Perks - Un instrument tractionnel pour la quadrature de l'hyperbole

Perks - Un instrument pour tracer la tractrice
En dehors de ses applications à la construction des courbes et à l'intégration des équations différentielles, la tractrice a joué un rôle surprenant dans le développement ultérieur de la géométrie. En effet, la surface de révolution engendrée par la rotation de la tractrice autour de son asymptote, surface appelée pseudosphère et étudiée par Beltrami en 1868, intervient dans l'interprétation de la géométrie de Lobachevski.
2. Tractrice et autres tractoires
Pour en savoir plus sur la tractrice :
http://chronomath.irem.univ-mrs.fr/chronomath/tractrice.htmlhttp://www-groups.dcs.st-and.ac.uk/~history/Curves/Tractrix.html
http://xahlee.org/SpecialPlaneCurves_dir/Tractrix_dir/tractrix.html
http://mathworld.wolfram.com/Tractrix.html
http://br.crashed.net/~glasnost/crc/math/t/t227.htm
[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires]