Le mouvement tractionnel en géométrie

3 - Application aux équations différentielles

Dès 1693, Leibniz a perçu l'intérêt du mouvement tractionnel pour l'intégration des équations différentielles. De façon générale, tracer une tractoire de base et de directrice données revient à construire une courbe inconnue dont les tangentes sont matérialisées par les positions successives d'un fil mobile. Si, par un dispositif mécanique adéquat, on arrivait à imposer qu'à chaque instant la direction du fil soit celle qui est fournie par le champ de vecteurs d'une certaine équation différentielle, on obtiendrait en fait une courbe intégrale de l'équation considérée.

Euler a repris cette idée en 1736 mais il s'est limité à l'emploi de tractoires ayant pour directrice un cercle de rayon constant (c'est-à-dire à l'utilisation d'un fil de longueur fixe). Cette limitation est compréhensible d'un point de vue pratique car seul un fil de longueur constante peut être facilement tiré le long d'une courbe donnée sur une feuille de dessin. Le cas d'un fil dont la longueur varie suivant une certaine loi nécessite des appareils mécaniques dont la mise au point est extrêmement délicate. En revanche, évidemment, se limiter à un fil de longueur constante ne permet d'intégrer que certaines classes relativement restreintes d'équations différentielles.

Pour pouvoir traiter davantage d'équations différentielles, il est indispensable de recourir à des tractoires ayant une directrice variable. C'est la voie qui a été explorée par Vincenzo Riccati en 1752 et qui a abouti, à la fin du 19e siècle, à la fabrication concrète d'intégraphes permettant d'intégrer graphiquement, avec une bonne précision, de larges classes d'équations comme les équations de Riccati ou les équations d'Abel.

Pour donner une idée de ces méthodes géométriques oubliées qui permettaient de résoudre de façon exacte de très nombreuses équations différentielles, et notamment des équations qui ne sont pas intégrables par quadratures, je vais développer un seul exemple, celui de l'équation de Riccati : y' = y² - x

J'ai choisi cet exemple car il a déjà été traité dans abraCAdaBRI par une autre méthode. De cette manière, le lecteur pourra comparer utilement une démarche géométrique ancienne à une démarche numérique moderne.

Soit y(x) une solution de l'équation différentielle y' = y2 - x. Considérons la courbe C d'équations :

Un calcul simple montre que la tangente à cette courbe C au point B(u(x), v(x)) coupe l'axe des abscisses au point A(x, 0).

Si on arrivait à tracer C en tant que tractoire ayant pour base l'axe des abscisses et pour directrice une courbe variable ne dépendant que de x, on pourrait en déduire y(x) par une construction simple à la règle et au compas (une fois qu'on connaît x, u(x) et v(x), on voit que y(x) = v(x)/(u(x)-x) est solution d'une équation du second degré). Or, si on pose

on vérifie sans difficulté que x(X-x)² = Y² - Y

Ainsi, le point B(u(x), v(x)) se trouve sur la conique liée à x et ayant pour équation x(X-x)² = Y² - Y. En résumé, la courbe C n'est autre qu'une tractoire ayant pour base l'axe des abscisses et pour directrice cette conique variable.

Finalement, pour obtenir une courbe intégrale de l'équation différentielle, il suffit de choisir une position initiale du fil (avec A₀ sur l'axe des abscisses et B₀ sur la directrice liée à A₀), de tracer la tractoire décrite ci-dessus (comme expliqué dans la partie 2.3), et de terminer en construisant le point (x, y(x)) à la règle et au compas à partir du point (u(x), v(x)).

Remarque : Dans la mise au point des macros " mouvement instantané " correspondant aux deux situations dont on va parler plus loin, il convient d'observer qu'une demi-droite rencontre parfois une conique en deux points et il faut donc veiller à montrer dans chaque cas le " bon " point ; si cela est fait correctement au départ, on ne rencontre pas de problème ultérieur car Cabri gère parfaitement le suivi des intersections.

On obtient divers types de courbes intégrales suivant que le fil est placé au-dessus ou au-dessous de l'axe des abscisses. La figure suivante montre d'abord le cas d'un fil placé au-dessus de l'axe des abscisses :

 

Riccati1.fig

Commentaire : Déplacer le point A le long de l'axe des abscisses. Le point B trace une tractoire à base rectiligne et à directrice conique variable. Le point C est construit à la règle et au compas à partir de A et B, et décrit une courbe intégrale de l'équation différentielle. Le tracé s'arrête à gauche et à droite lorsque la longueur du fil AB devient infinie. On réalise ainsi toutes les courbes intégrales à pente négative, c'est-à-dire celles situées à l'intérieur de l'isocline 0, qui n'est autre que la parabole d'équation y² = x.

En traçant de cette manière dix courbes intégrales pour dix positions initiales du fil, on obtient une bonne image de ce qui se passe à l'intérieur de l'isocline 0 :

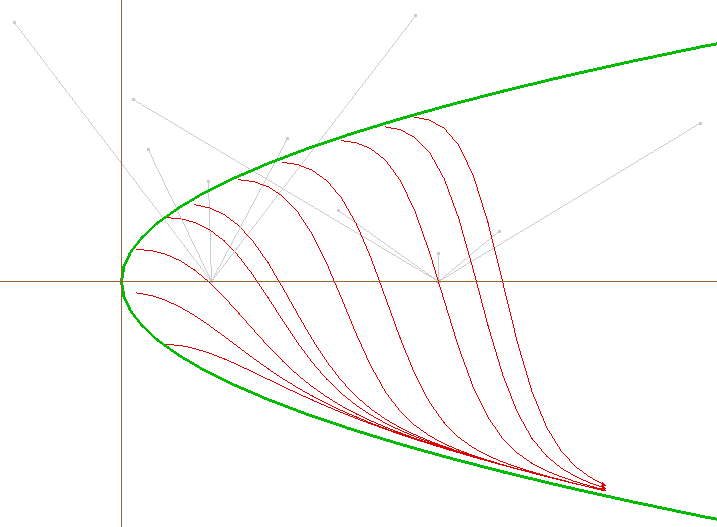
Riccati2.fig (la figure est longue à ouvrir)

Passons maintenant au cas où le fil est placé au-dessous de l'axe des abscisses. Sur la figure suivante, on peut observer deux comportements distincts pour les courbes intégrales :

Riccati3.fig

Commentaire : Lorsque le fil est au-dessous de l'axe des abscisses, on obtient deux types de courbes intégrales à pente positive :

• des courbes (en rose) ayant deux asymptotes verticales, avec un tracé qui s'arrête à gauche et à droite lorsque la longueur du fil devient nulle ;
• des courbes (en bleu) ayant une asymptote verticale à gauche et une tangente horizontale à droite, avec un tracé qui s'arrête à gauche lorsque la longueur du fil devient nulle et à droite lorsque cette longueur devient infinie.

Déplacer le point A (rose ou bleu) pour observer comment ces courbes intégrales sont décrites par le point C (rose ou bleu).

Terminons en traçant à nouveau une dizaine de courbes intégrales pour visualiser ce qui se passe à l'extérieur de l'isocline 0 :

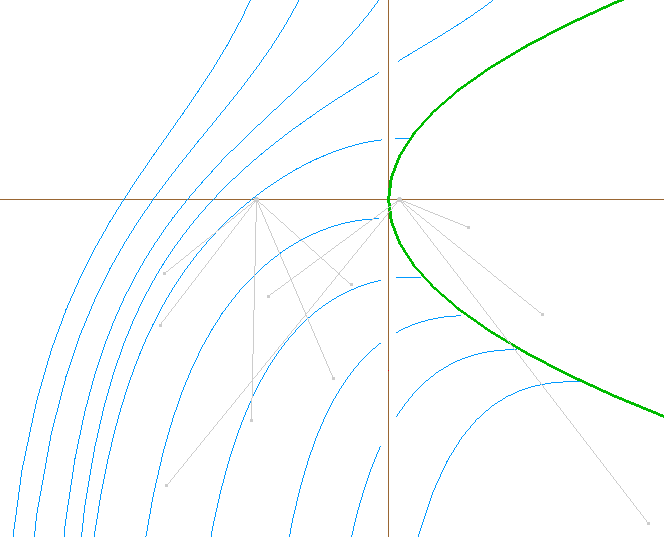
Riccati4.fig (la figure est longue à ouvrir)

En faisant abstraction de la simulation du mouvement tractionnel à laquelle j'ai été obligé de recourir dans Cabri, il faut prendre conscience du fait que ces constructions sont exactes. Elles témoignent du savoir faire éblouissant des géomètres du 18e siècle, qui ont porté à son aboutissement ultime la riche tradition géométrique héritée des Grecs et des Arabes. Après 1750, ce savoir faire va peu à peu tomber dans l'oubli et les mathématiques vont entrer dans la seconde phase de leur histoire : la phase algébrique, qui est encore la nôtre aujourd'hui.

Menu général