[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires] [Application aux équations différentielles]
[Tractrice et pseudo-sphère] [Retour "Courbes et équations"]
Dans tout ce qui précède, on a supposé que la longueur du fil était constante (égale à a). Cette hypothèse est-elle vraiment indispensable ? Où intervient-elle exactement dans la construction ?
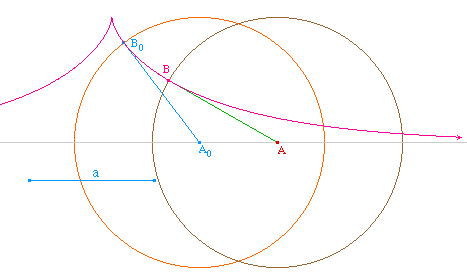
Quand on utilise la propriété AB = a, cela signifie simplement que le point B se trouve sur le cercle de centre A et de rayon a. Autrement dit, une longueur a étant donnée, on attache au point A un cercle de rayon a, cercle que le point A entraîne dans son déplacement le long de la base. Et c'est finalement ce cercle mobile qui modélise la contrainte imposée au fil de garder une longueur constante au cours du mouvement.

On peut généraliser de façon naturelle en remplaçant le cercle précédent par une courbe quelconque liée à A et l'accompagnant de même au cours de son déplacement. Cette courbe sera appelée directrice de la tractoire. En quelque sorte, la directrice va servir à modéliser la loi de variation de la longueur du fil au cours du mouvement. Concrètement, si l'on voulait fabriquer un appareil tractionnel réel, on pourrait prévoir une bobine dont le fil se déviderait en étant guidé par un gabarit ou un système articulé.
La macro initiale TractInst.mac, sur laquelle reposaient toutes les constructions des parties précédentes, est à modifier comme suit : pour passer d'une position AB du fil à la position suivante A'B', on construisait B' comme intersection de la demi-droite [AB) et du cercle de centre A' et de rayon a ; il suffit maintenant de construire B' comme intersection de la demi-droite [AB) et de la courbe directrice liée à A'. Bien-sûr, il est utile de préparer une macro intermédiaire qui, à un point de la base, associe la courbe qui lui est liée, ne serait-ce que pour tracer cette courbe.
Pour fixer la position initiale du fil, on doit choisir un point A0, puis un point B0 sur la directrice liée à A0.
Une fois modifiée la macro initiale, le reste ne change pas. Voici, à titre d'exemple, une tractoire de base rectiligne et de directrice une hyperbole équilatère (plus précisément, une longueur a étant donnée, la directrice liée au point courant A est l'hyperbole équilatère de centre A, d'axe perpendiculaire à la base et de demi-axe a).

1) on tire l'extrémité A le long d'une courbe quelconque donnée (la base) ;
2) l'extrémité traçante B est astreinte à demeurer sur une courbe quelconque donnée liée à A et l'accompagnant dans son mouvement (la directrice).
Une question naturelle vient alors à l'esprit : quelles courbes peut-on obtenir en tant que tractoires ? En particulier, les courbes représentatives des fonctions usuelles peuvent-elles être construites ainsi ? On a vu dans la partie 2.2.b (en détaillant l'exemple de la parabole) que l'on pouvait effectivement faire apparaître la courbe représentative d'une fonction comme tractoire à directrice circulaire d'une courbe paramétrée. Mais ce résultat n'est pas satisfaisant car, en général, la courbe paramétrée servant de base est plus compliquée à construire que la courbe cherchée, voire n'est même pas constructible à la règle et compas.
Il serait judicieux de remettre le problème en chantier en exploitant la possibilité nouvelle de faire varier la directrice. Je propose donc, à présent, de conserver une base rectiligne et de chercher à jouer plutôt sur la directrice.
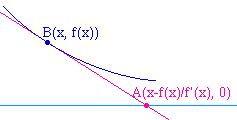 |
Soit donc une courbe d'équation y = f(x). La tangente issue du point B, de coordonnées (x, f(x)), coupe l'axe des abscisses au point A, de coordonnées (x-f(x)/f '(x), 0) . Si on pose u = x - f(x)/f '(x), de sorte que le point A ait pour coordonnées (u, 0), tout revient à trouver une courbe ne dépendant que de u et à laquelle appartienne le point B. |
Prenons l'exemple d'une fonction puissance (avec n rationnel). Dans ce cas, on a :
Le point B, de coordonnées ![]() se trouve donc sur la droite d'équation
se trouve donc sur la droite d'équation ![]() . Cette droite, qui ne dépend que de A, peut être
associée au point A et servir de directrice.
. Cette droite, qui ne dépend que de A, peut être
associée au point A et servir de directrice.
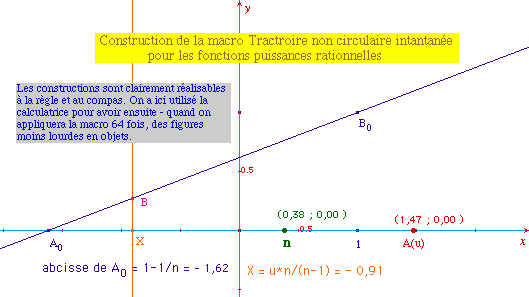
On en déduit la figure suivante :
![]() FRenT16p.fig et FRenTR16.mac
mais aussi FRenTR64.mac
FRenT16p.fig et FRenTR16.mac
mais aussi FRenTR64.mac
|
|
On obtient ainsi toutes les fonctions puissances en tant que tractoires à base rectiligne et à directrice rectiligne. La figure permet d'expérimenter agréablement : on peut faire varier la puissance n, on peut déplacer soi-même l'extrémité A du fil, on peut tracer sur la même figure la fonction puissance obtenue avec la calculatrice afin d'évaluer la précision, on peut reprendre avec des partages en 32 et 64, etc. Voici quelques figures correspondant aux cas les plus usuels. Ci contre, pour n = 2, la fonction carré. Remarque : en pratique, pour lisser les courbes au voisinage de l'origine, il est préférable de prendre A sur un segment.
|
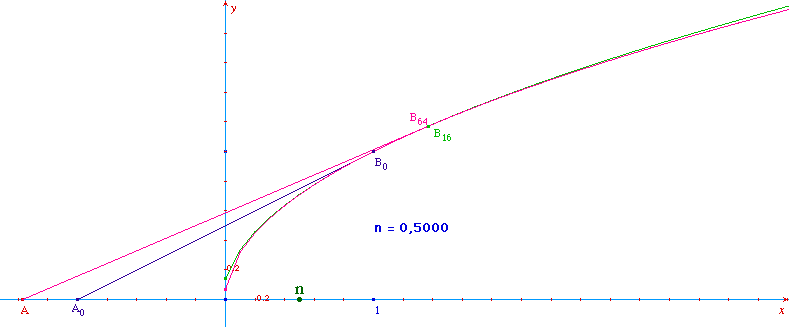
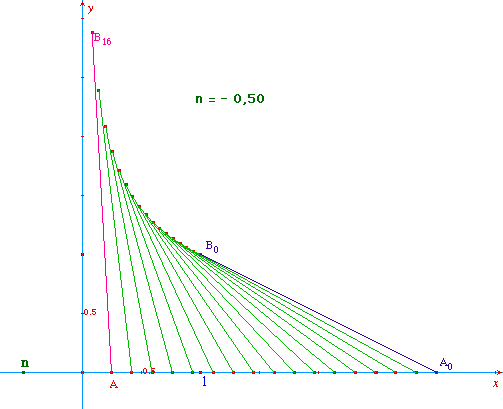
Illustration de la même figure pour n = 1/2 ...
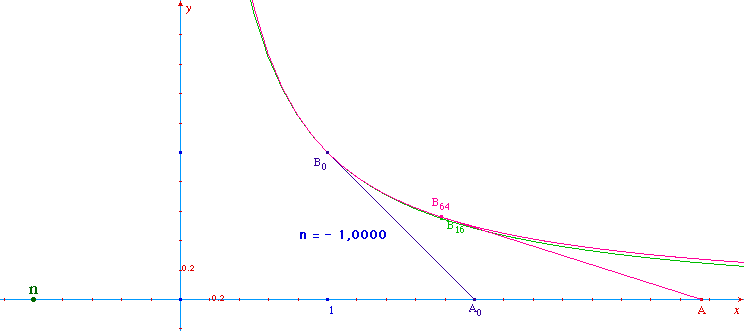
... et pour n = -1
Il serait tentant d'étendre ce travail à d'autres fonctions usuelles, en particulier à des fonctions transcendantes. En effet, le mouvement tractionnel est un phénomène physique simple et naturel que l'on reçoit volontiers en géométrie dans la mesure où il permet de tracer des courbes d'un mouvement continu (ce qui a toujours été préféré à la construction de courbes par points : dans une construction par points, on n'obtient que des points particuliers de la courbe, à partir desquels le tracé se fait à vue, par interpolation, alors que dans un tracé effectué d'un mouvement continu, on considère qu'on atteint de façon exacte tous les points de la courbe). Si donc on pouvait construire les fonctions transcendantes usuelles en tant que tractoires, cela conduirait à accepter ces fonctions en géométrie en tant que fonctions constructibles.
Malheureusement, Cabri ne sait pas trouver l'intersection d'un lieu et d'une droite, ce qui oblige à n'employer comme directrices que des droites, cercles ou coniques. On pourrait, par exemple, montrer que les fonctions trigonométriques sont des tractoires ayant pour directrices des courbes algébriques simples constructibles à la règle et au compas, et donc accéder à des constructions exactes des lignes trigonométriques, mais Cabri nous l'interdit actuellement.
Dans cette situation, on ressent cruellement l'absence d'un solveur d'équation (sous la forme d'une touche " solve " à incorporer dans la calculatrice). Il est frustrant de voir sur l'écran le point d'intersection d'un lieu et d'une droite et de ne pouvoir utiliser ce point pour des constructions ultérieures. Avec un solveur d'équation, on pourrait au moins calculer soi-même les coordonnées du point d'intersection à partir des équations du lieu et de la droite, et s'en servir pour placer le point sur la figure.
En attendant qu'une prochaine version de Cabri nous offre ce solveur tant désiré, je laisse à la réflexion des lecteurs la possibilité éventuelle d'imaginer un moyen détourné pour construire les fonctions trigonométriques en tant que tractoires.
Par contre, en guise de consolation, les fonctions exponentielles et logarithmes ne soulèvent pas autant de difficultés et sont constructibles facilement : ce sera l'objet de la partie 2.4.
[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires] [Application aux équations différentielles]
[Tractrice et pseudo-sphère] [Retour "Courbes et équations"]