Le mouvement tractionnel en géométrie

2 - Tractrice et autres tractoires

2.1. Construction de la tractrice

Construction pour un point voisin

 

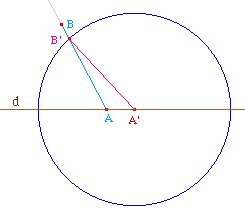
Considérons la droite de base d et une position AB du fil (de longueur a) à un instant donné. À l'instant suivant, le fil occupe la position A'B'. Le point A' étant donné, comment construire le point B' ? La position de B' est déterminée par ces deux remarques : la longueur A'B' est encore égale à a ; le mouvement instantané BB' se fait le long de la tangente (AB) à la tractrice, plus précisément sur la demi-droite [AB) puisque B' reste voisin de B. Autrement dit, B' est l'intersection de la demi-droite [AB) et du cercle de centre A' et de rayon AB = a. On peut donc enregistrer une première macro, TractInst.mac, ayant pour objets initiaux le point A, le point B et le point A', et pour objet final le point B'.

Si on examine cette construction d'un point de vue analytique, en notant (x, y) les coordonnées du point générique B de la tractrice, et les coordonnées du point voisin B', on observe que :

Autrement dit, la construction revient à remplacer l'équation différentielle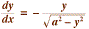  

par l'équation aux différences finies :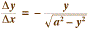

Ce n'est rien d'autre que la méthode d'Euler, sauf que le pas 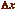n'est pas fixé à l'avance et une fois pour toutes, mais s'adapte dynamiquement sous la contrainte géométrique que la longueur du fil doit rester constante.

Dans mon approche, il n'y a en fait ni équation différentielle, ni calcul 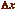de et de 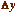(même si, après coup, on peut interpréter la construction en ces termes). Je ne fais pas une intégration " numérique ", mais une intégration " géométrique " en ce sens que la construction respecte à chaque pas les propriétés fondamentales du mouvement : constance de la longueur du fil, mouvement instantané le long de la tangente réelle.

Si on appliquait la méthode d'Euler classique, on obtiendrait certes une tractrice approchée, mais la longueur du fil varierait légèrement au cours du processus : l'œil s'en apercevrait et notre cerveau aurait du mal à accepter le mouvement approché comme un bon modèle du mouvement réel. Avec la méthode géométrique, on est certain que le fil va garder une longueur constante, d'où une simulation convaincante du mouvement tractionnel, et ce indépendamment de la précision réelle de la construction.

On peut noter au passage que cette intégration géométrique est tout à fait dans l'esprit de certaines recherches récentes en analyse numérique, qui ont tendance à s'éloigner du calcul numérique brut et aveugle pour redonner un sens géométrique aux algorithmes utilisés. D'une certaine façon, on préfère travailler sur l'allure globale de la solution plutôt qu'améliorer la précision locale de façon illusoire et coûteuse.

Construction infinitésimale dynamique

Après avoir vu comment passer d'un point à un point " infiniment " voisin, comment passer à un point éloigné ? Soit A₀B₀ la position initiale du fil et soit A un point quelconque de la droite d. On partage le segment [A₀A] en 16 parties (16 est largement suffisant pour une première approche, 32 voire 64 parties peuvent être utiles dans certaines constructions plus élaborées demandant davantage de précision) et on applique 16 fois la macro TractInst.mac.

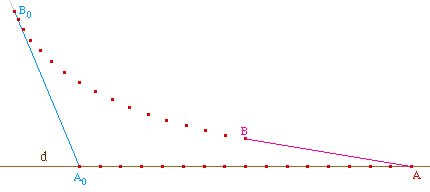
Tract16p.fig ou la macro associéeTract16p.mac,
d' objets initiaux A₀, B₀ et le point A, et d'objet final le point B.

A partir de cette construction, il est facile de poursuivre pour réaliser les macros Tract32p.mac ou Tract64p.mac pour des partages en 32 ou 64 parties.

Pour obtenir la tractrice, on oublie ce qui précède, on repart d'un point A de la droite d, on construit le point B avec la macro précédente et on demande le lieu de B lorsque A décrit la droite d. C'est une construction dynamique en ce sens que la ligne polygonale à 16 côtés est entièrement reconstruite pour chaque point A de la droite d. Le résultat est qu'on obtient une courbe parfaitement lisse, et non une ligne brisée.

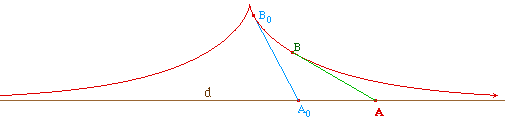
Tractr01.fig

La figure se prête à diverses manipulations : en tirant le point A le long de la droite d de la gauche vers la droite à partir de A₀, on simule le mouvement d'un fil réel (au sens strict, il ne faudrait pas tracer la partie de la courbe correspondant à des positions de A à gauche de A₀ car il ne se passe rien avant l'instant initial, c'est-à-dire avant l'instant où la main commence à tirer le fil) ; par ailleurs, on peut modifier les positions initiales de A₀ et/ou de B₀, notamment pour observer l'effet de diverses longueurs de fil.

Précision de la construction

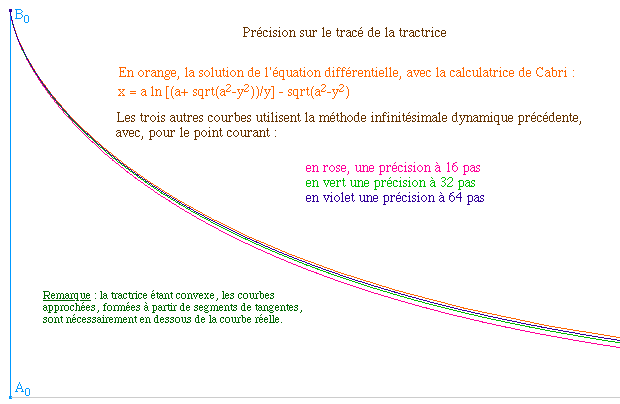
Pour évaluer expérimentalement la précision de cette construction " infinitésimale dynamique ", on peut construire la partie droite de la tractrice de diverses façons :

Tract02.fig

La chaînette, développée de la tractrice

Une fois que l'on sait construire la tractrice, on peut explorer avec Cabri les propriétés de la courbe décrites dans les traités classiques. En guise d'exemple, intéressons-nous à la développée de la tractrice, qui n'est autre que la chaînette (d'équation y = ch x lorsque a = 1, c'est-à-dire lorsqu'on prend la longueur du fil pour unité).

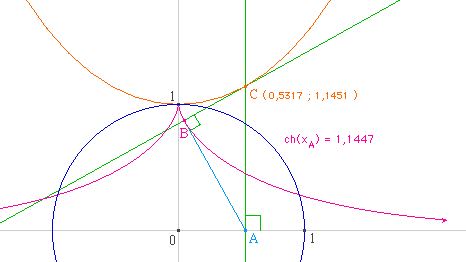
Le fil AB donne la direction de la tangente. La perpendiculaire en B à AB est donc la normale à la courbe. Le centre de courbure C est à l'intersection de la normale et de la perpendiculaire en A à la base.

Pour obtenir la développée de la tractrice, il suffit alors de demander le lieu du centre de courbure C lorsque A décrit la base. Dans Cabri, on pourra demander à titre de vérification le lieu de la droite (BC) lorsque A décrit la base, car la développée est aussi l'enveloppe des normales. Les deux lieux sont quasiment indiscernables à l'écran (même pour un partage en 16), et leur écart est une autre façon de mesurer le défaut de construction de la tractrice.

Enfin, il est intéressant de comparer l'ordonnée du point C avec la valeur de la fonction ch fournie par la calculatrice (ci-dessous faite avec un partage en 64).

Tract03.fig

 

Pour des précisions sur les développées et développantes en général et sur le cas de la tractrice en particulier, voir :

http://chronomath.irem.univ-mrs.fr/Courbes/devppante.html

Menu général