[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires] [Application aux équations différentielles]
[Tractrice et pseudo-sphère] [Retour "Courbes et équations"]
J'ai dit dans la partie 1 que la connaissance de la tractrice permettait de réaliser la quadrature de l'hyperbole, c'est-à-dire de construire les logarithmes. Le moment est venu de préciser cette affirmation.
Considérons une tractrice construite au moyen d'un fil AB de longueur unité, de sorte qu'à l'instant initial, le fil soit placé le long de l'axe des ordonnées, avec une extrémité en (0, 0) et l'extrémité traçante en (0, 1). La partie droite de la courbe, correspondant aux abscisses positives, a pour équation :
Posons 
.
Lorsque y décrit l'intervalle ]0,1], z décrit
l'intervalle 
,
et on a 
. Si, au point courant B de la tractrice, de coordonnées (x,
y), on associe le point d'abscisse z (ce nombre est constructible
facilement à la règle et au compas à partir de
y) et d'ordonnée OA (il suffit de reporter sur l'axe des
ordonnées l'abscisse de l'extrémité A du fil),
on obtient un point de coordonnées (z, ln z) qui décrit
la partie de la courbe logarithmique correspondant à z
supérieur ou égal à 1.
(Ci dessous, pour diminuer le nombre d'objets, la partie
constructible a été réalisée à la
calculatrice)
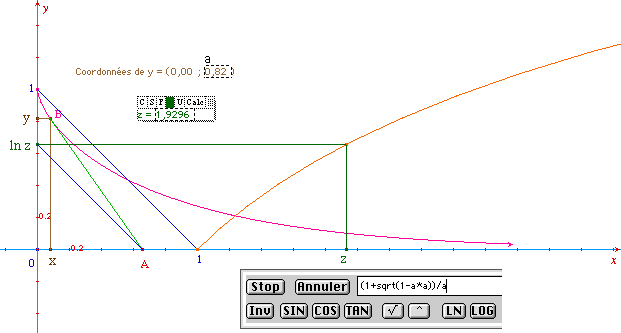
Par ailleurs, la partie gauche de la tractrice a pour équation :
Cette fois, on pose 
et z décrit l'intervalle ]0, 1] lorsque y
décrit l'intervalle ]0,1].
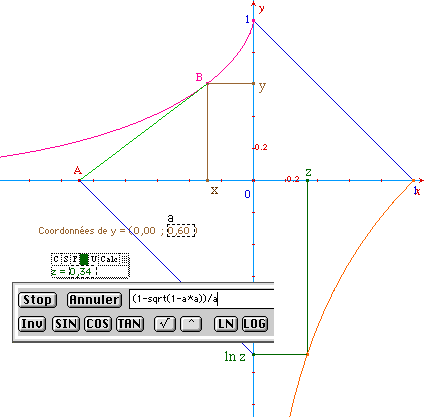
On a maintenant 
,
d'où une construction tout à fait analogue à la
précédente pour la partie de la courbe logarithmique
correspondant à z inférieur ou égal à 1.
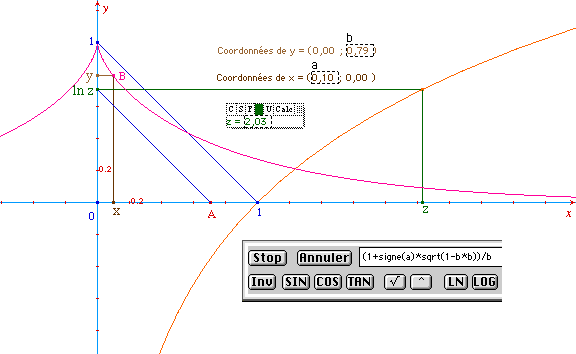
En fait, dans Cabri, on peut réaliser une seule construction valable pour toute la courbe. Il suffit d'associer au point courant B de la tractrice, de coordonnées (x, y), le point de coordonnées :
Ce point décrit la courbe logarithmique népérienne, courbe qui est donc constructible si l'on dispose d'une règle, d'un compas et d'un fil de longueur unité.
Si, sur une feuille de papier, on traçait la tractrice d'un mouvement continu avec un vrai fil, la construction serait exacte (du moins en théorie, en oubliant l'imperfection matérielle de la règle, du compas et de l'instrument tractionnel concrètement utilisés). Mais, dans Cabri, on ne trace pas réellement la tractrice : on se contente de simuler le mouvement par la méthode infinitésimale dynamique décrite dans la partie 2.1. Par suite, il y a une erreur de méthode qu'il est intéressant d'évaluer.
Dans les figures précédentes, on a construit les logarithmes au moyen d'une tractrice approchée réalisée avec un partage en 64. En comparant avec la fonction de la calculatrice, on peut aprécier la précision :
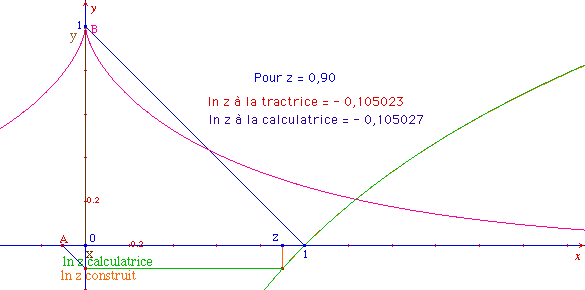
Lorsque le fil est proche de sa position initiale, c'est-à-dire lorsque z est voisin de 1, la précision est remarquable
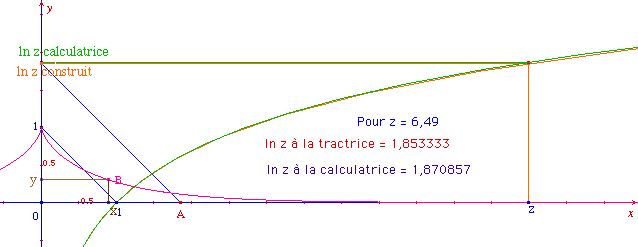
Lorsque le fil s'éloigne de sa position initiale, la précision se dégrade progressivement comme il fallait s'y attendre
Dans cette première construction des logarithmes, on a utilisé la tractrice comme courbe auxiliaire : autrement dit, une fois la tractrice tracée sur la feuille de papier, les logarithmes deviennent constructibles à la règle et au compas.
Une autre approche vient de la théorie développée dans la partie 2.3 : ne pourrait-on pas obtenir la courbe logarithmique directement comme tractoire, en prenant une base rectiligne et une directrice convenable à déterminer ?
 |
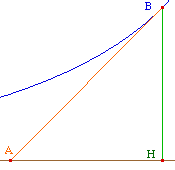L'analyse est plus facile en partant des fonctions exponentielles. Soit donc la courbe d'équation y =bx (b strictement positif, et différent de 1). Un point B de la courbe a pour coordonnées (x, bx ). La tangente en B coupe l'axe des abscisses au point A de coordonnées (x - 1/ln b, 0). Le point H, projeté orthogonal de B sur l'axe des
abscisses, a pour coordonnées (x, 0), et donc le
vecteur |
La mesure algébrique 
n'est
autre que la sous-tangente du point B, et ce qui
précède ramène à une
caractérisation géométrique bien connue des
courbes exponentielles :
Les courbes ayant une sous-tangente constante égale à 1/ln b sont exactement les courbes d'équation y = C.bx, où C est une constante non nulle déterminée par la valeur initiale y(0).
De notre point de vue, ce qui est intéressant, c'est que le
point B se trouve sur la perpendiculaire à l'axe des abscisses
passant par le point H tel que 
. On a ainsi trouvé une courbe ne dépendant que de A et
pouvant servir de directrice pour le tracé d'une tractoire.
Pour construire les courbes logarithmiques, il ne reste plus
maintenant qu'à voir le problème à l'envers, via
une symétrie par rapport à la première
bissectrice.
LNTRInst.fig et LNTRInst.mac
puis LNTR16p.fig (ci-dessus) et
enfin LNTR16p.mac
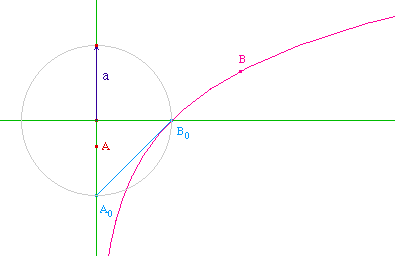
Partons d'une droite verticale qui sera la base de la tractoire et
donnons-nous sur cette droite un vecteur non nul de longueur a.
Prenons un fil placé dans la position initiale
A0B0. À un point A quelconque de la
base, associons (en tant que directrice) la perpendiculaire à
la base passant par le translaté de A dans la translation de
vecteur donné. Construisons avec ces éléments
une tractoire conformément à la théorie de la
partie 2.3. Cette tractoire n'est autre
qu'une courbe logarithmique de base b, avec b tel que 
,
ou encore b = exp(1/a).
 |
Si l'on veut construire plus spécifiquement la fonction logarithme népérien dans un repère donné à l'avance, il suffit de choisir a = 1 et de fixer la position initiale du fil de sorte que soit satisfaite la condition initiale f(1) = 0.
|
Evaluation graphique de l'erreur par comparaison avec la calculatrice
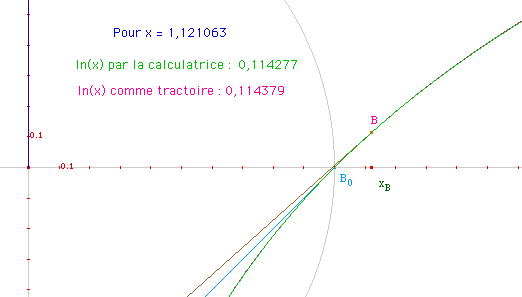
Remarquable précision au voisinage de la condition initiale ...
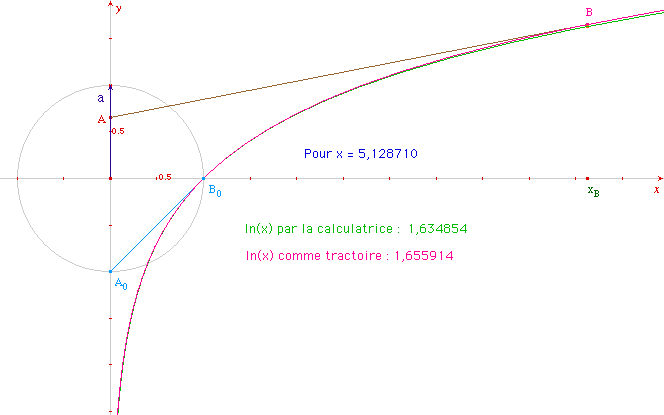
... qui s'éffrite un peu pour des valeurs plus éloignées
Cette seconde construction des logarithmes, plus directe que la première, est belle et pure. En s'en inspirant, il est envisageable de fabriquer un appareil mécanique pour tracer concrètement les courbes logarithmiques d'un mouvement continu, de la même manière que le compas permet de tracer les cercles d'un mouvement continu. À partir de là, rien ne s'oppose plus à ce que les courbes logarithmiques soient considérées comme " géométriques " au même titre que les cercles.
Chers lecteurs d'abraCAdaBRI, vous qui regardiez les logarithmes avec méfiance, vous qui hésitiez à employer des nombres tirés de lourdes tables désuètes ou issus d'obscurs algorithmes numériques, n'ayez plus de scrupules : soyez beaux joueurs et acceptez les logarithmes en géométrie ! Désormais, lorsque vous appuierez sur la touche " ln " de la calculatrice de votre logiciel préféré, vous pourrez faire comme si c'était l'abréviation d'une construction géométrique exacte, réalisée indépendamment de toute considération numérique.
Depuis le début de ce dossier, l'un dans l'autre, j'ai essayé de faire sentir au lecteur que les fonctions élémentaires (puissances, trigonométriques, logarithmiques et exponentielles) pouvaient être acceptées en géométrie en tant que fonctions constructibles, à condition d'adjoindre le mouvement tractionnel aux procédés classiques de construction.
Une immense perspective s'ouvre alors au géomètre éclairé : en prenant pour base et pour directrice des courbes déjà construites, on peut construire de nouvelles tractoires… et recommencer autant de fois que l'on veut, chaque étape augmentant de fait le stock des courbes constructibles.
Grâce à cette pléïade de nouvelles courbes, il sera peut-être possible de construire, dans la partie 3, les solutions de nouvelles équations différentielles (on pense en priorité aux équations qui résistent à la méthode traditionnelle de construction par quadratures).
[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires] [Application aux équations différentielles]
[Tractrice et pseudo-sphère] [Retour "Courbes et équations"]
Menu général
est
un vecteur constant, de coordonnées (1/ln b, 0)