Le mouvement tractionnel en
géométrie
4 - Tractrice et
pseudo-sphère
4.1. Un peu
d'histoire
4.1. Un peu d'histoire | 4.2.
Construction : Parallèles et méridiens
4.3. Géométrie
intrinsèque de la pseudosphère | 4.4.
Modèle de Beltrami sur la pseudosphère
4.5. Conjugaison entre la pseudosphère
et le plan
[Introduction] [Histoire
de la tractrice] [Tractrice et
autres tractoires]
[Application aux équations
différentielles] [Tractrice et
pseudo-sphère] [Retour
"Courbes et équations"]

|
Résumé :
Aprés avoir été utilisée pour
l'intégration graphique d'équations
différentielles, la tractrice, en changeant de
dimension, va vivre une nouvelle vie,
particulièrement riche : en tournant sur sa base, la
tractrice engendre une surface de révolution qui va
être à l'origine de bien des
développements. Beltrami lui a donné le nom de
pseudo-sphère. Et il a montré que localement
la pseudo-sphère se comporte comme un plan
hyperbolique, au sens de Lobatchevsky. Beltrami avait ainsi
réalisé pour la première fois, en 1868,
un modèle réel de géométrie non
euclidienne. Et même si ce modèle n'est que
local, il a joué un rôle important dans la
diffusion de la géométrie non euclidienne : on
avait désormais la possibilité de se
représenter les figures hyperboliques sur une
surface.
Cette page se propose de reprendre dans ses grandes
lignes, les idées générales qui ont
amené Beltrami à réaliser que les
surfaces pseudo-sphériques modèlisaient la
géométrie hyperbolique.
|
|
Beltrami s'inscrit dans la recherche - bien active alors
en Italie - sur la géométrie
différentielle intrinsèque des surfaces,
inaugurée par Gauss en 1827.
En 1863, professeur de géodésie à
l'université de Pise, il s'intéresse à
la représentation d'une surface sur un plan, en
cherchant à généraliser, avec les
outils développés par Gauss, d'anciens
résultats de Lagrange.
|

|
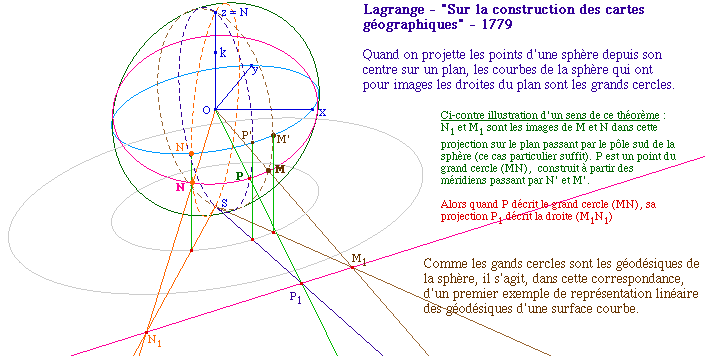
Beltrami se propose de reprendre cette idée en la
généralisant et se pose la question de savoir quelles
sont les surfaces pour lesquelles les géodésiques -
lignes de plus courte distance - soient décrites de
manère linéaire (on dit parfois "par des droites").
Plus précisément, si on note X et Y les
coordonnées curvilignes d'une surface ayant une
représentation dans le plan euclidien (x, y) avec x = u(X, Y)
et y = v(X, Y), les géodésiques de la surface seront
représentées dans le plan par des droites ax + by + c =
0 ssi la courbe représentée en coordonnée
curviligne par au(X, Y) + bv(X, Y) + c = 0 est bien une
géodésique de cette surface.
En 1865, il publie un premier résultat : le problème
n'a pas de solution générale, il n'est possible que
dans des cas particuliers :
"...les seules surfaces
succeptibles d'être représentées sur un plan,
en sorte qu'à chaque point de l'une corresponde un point de
l'autre et qu'à chaque ligne géodésique
corresponde une ligne droite, sont celles dont la courbure est
partout constante (positive, négative ou
nulle)."
D'où l'intérêt pour les surfaces
pseudo-sphèriques - celles dont le rayon de courbure est
constant, que l'on peut noter -1/R2. Il n'est pas le
premier à s'y intéresser puisque dès 1839,
Minding se penche sur la question et trouve des formules
trigonométriques qui, aux notations près sont celle de
la jeune "géométrie imaginaire" (plane) de Lobachevsky.
Mais le lien profond entre la géométrie
intrinsèque des surfaces à courbure constante
négative et le plan hyperbolique n'est pas fait.
C'est parce qu'il cherchait une représentation
linéaire des géodésiques que Beltrami trouva ce
lien. Compte tenu des relations auxquelles il aboutit sur les
abscisses curvilignes, Beltrami est amené à
représenter une partie de la surface qu'il étudie par
l'intérieur d'un cercle - qu'il appelle cercle limite, les
géodésiques de la surface devenant alors les cordes de
ce cercle. Il découvre ainsi les premières
règles de ce qui deviendra ultérieurement le
modèle dit "de Klein-Beltrami" quand Klein lui donnera sa
dimension projective tout en le liant à la métrique
absolue de Cayley. Voici ce qu'il écrit dans son
interprétation de 1868 :
|
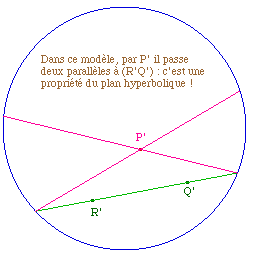
|
1 - A deux cordes distinctes qui se coupent à
l'intérieur du cercle limite correspondent deux
lignes géodésiques qui se coupent en un point
à une distance finie, sous un angle différent
de 0 et de 180 degrés.
2 - A deux cordes distinctes qui se coupent sur la
circonférence du cercle limite correspondent deux
lignes géodésiques qui concourent vers un
même point à une distance infine, et qui font
en ce point un angle nul.
3 - Enfin, à deux cordes qui se coupent hors du
cercle limite, ou qui sont parallèles, correspondent
deux lignes géodésiques qui n'ont aucun point
commun dans toute l'étendue (réelle) de la
surface.
|
Sans entrer dans des détails trop techniques - une autre
partie du site y sera consacrée - disons que c'est en
s'intéressant aux circonférences
géodésiques que Beltrami s'aperçoit, dans le cas
d'un centre à l'infini, d'une part que ces cercles se
comportent comme les horicycles de Lobachevsky et d'autre part que la
surface est alors elle ainsi un cas bien particulier : il est
amené à introduire ce qu'il nomme lui-même
la pseudosphère, surface de
révolution dont les méridiens sont une tractrice.
Ce premier modèle est assez complexe, si on le compare
à ceux qui seront élaborés par la suite. En
effet, la pseudosphère ne correspond pas au plan hyperbolique,
ni même à un horicycle, mais seulement à un
secteur d'un horicycle. C'est l'enroulement infini de la
pseudo-sphère sur elle-même qui correspond à un
horicycle entier. Ainsi la pseudosphère n'est-elle en
bijection qu'avec une partie bien limitée du plan hyperbolique
: la pseudosphère n'est que localement isométrique
à un plan hyperbolique.
En 1901 - soit un an après la mort de Beltrami - Hilbert
montrera qu'on ne peut généraliser :
"[dans l'espace
eucldien] il n'existe aucune surface à courbure
constante négative dépourvue de singularité,
analytique, et partout régulière. En particulier, on
doit répondre par la négative à la question
soulevée au début, à savoir qu'il n'existe
pas dans l'espace une telle surface, sur laquelle, à la
manière de Beltrami, la géométrie du plan de
Lobachevsky se trouve entièrement
réalisée."
Enfin, signalons que Beltrami s'est aussi
intéréssé à la construction effective
d'une pseudosphère. Il en a réalisé plusieurs
exemplaires méticuleusement, pour pouvoir mieux visualiser les
géodésiques.
Nous allons nous, faire cela avec Cabri ...
4.1. Un peu d'histoire | 4.2.
Construction : Parallèles et méridiens
4.3. Géométrie
intrinsèque de la pseudosphère | 4.4.
Modèle de Beltrami sur la pseudosphère
4.5. Conjugaison entre la pseudosphère
et le plan
[Introduction] [Histoire
de la tractrice] [Tractrice et
autres tractoires]
[Application aux équations
différentielles] [Tractrice et
pseudo-sphère] [Retour
"Courbes et équations"]
 Menu général
Menu général



