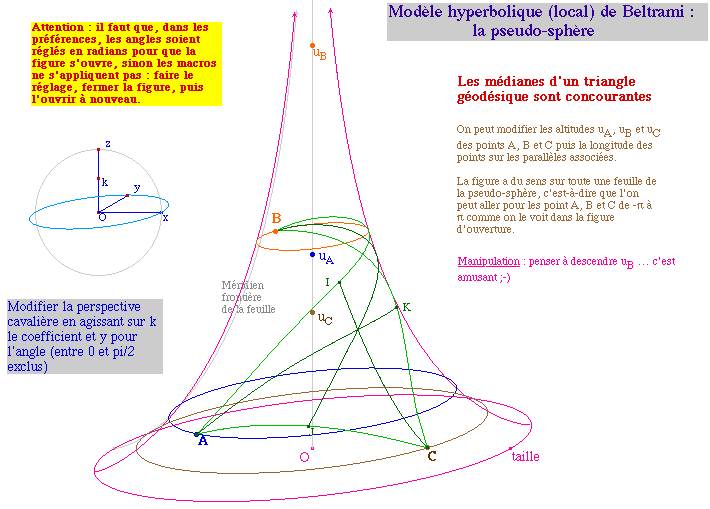
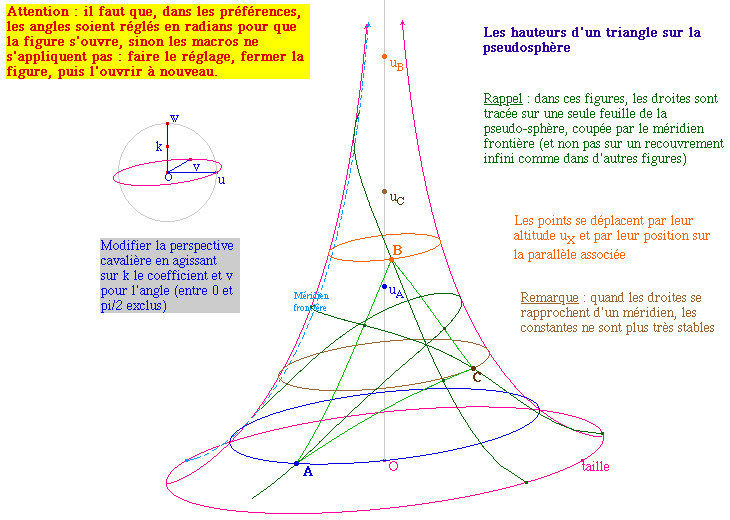
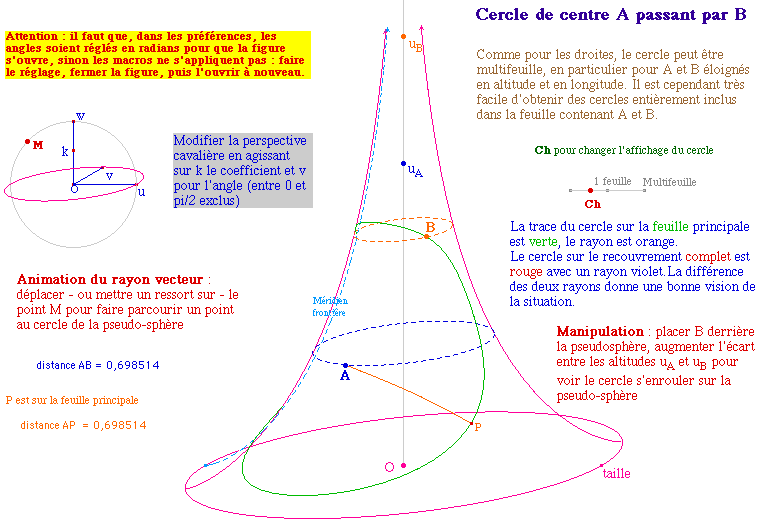
![]() PSCercle.fig
Quand M décrit le cercle de
référence P - ou Q sur la seconde feuille -
décrit le cercle pseudosphèrique
PSCercle.fig
Quand M décrit le cercle de
référence P - ou Q sur la seconde feuille -
décrit le cercle pseudosphèrique
[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires]
[Application aux équations différentielles] [Tractrice et pseudo-sphère] [Retour "Courbes et équations"]
Voici quelques figures intéressantes à manipuler :



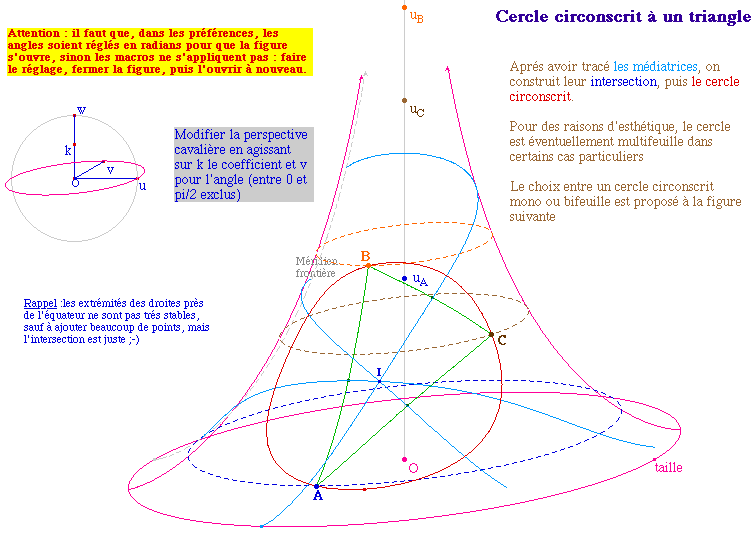
![]() PSCercle.fig
Quand M décrit le cercle de
référence P - ou Q sur la seconde feuille -
décrit le cercle pseudosphèrique
PSCercle.fig
Quand M décrit le cercle de
référence P - ou Q sur la seconde feuille -
décrit le cercle pseudosphèrique


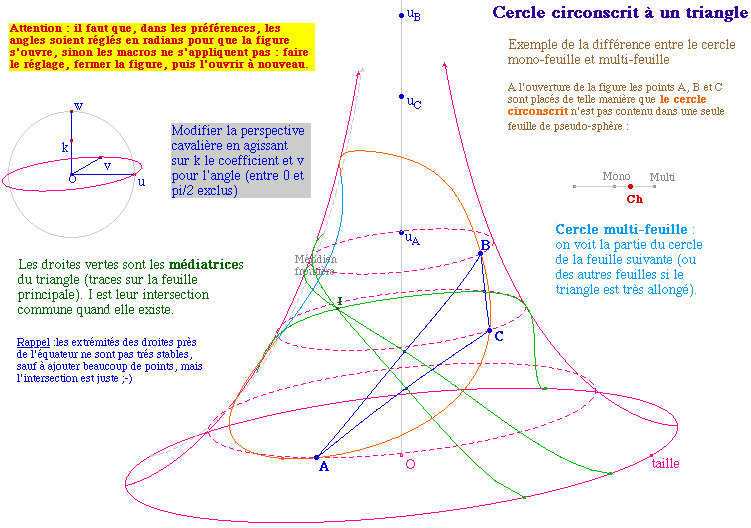
la page suivante (4.5) est encore plus délirante ;-)
4.1. Un peu d'histoire | 4.2.
Construction : Parallèles et méridiens
4.3. Géométrie
intrinsèque de la pseudosphère | 4.4. Modèle
de Beltrami sur la pseudosphère
4.5. Conjugaison entre la pseudosphère
et le plan
[Introduction] [Histoire de la tractrice] [Tractrice et autres tractoires]
[Application aux équations différentielles] [Tractrice et pseudo-sphère] [Retour "Courbes et équations"]