Le mouvement
tractionnel en géométrie
2 - Tractrice et autres
tractoires
2.2.a Tractoire à base
circulaire
2.1 Construction de la tractrice |
2.2. Tractoire à base non rectiligne
2.3. Tractoire à directrice non
circulaire | 2.4. Construction des
logarithmes
[Introduction] [Histoire
de la tractrice] [Tractrice et autres tractoires]
[Application aux équations
différentielles]
[Tractrice et
pseudo-sphère] [Retour
"Courbes et équations"]
La tractrice est, rappelons-le, la courbe décrite par
l'extrémité libre B d'un fil de longueur constante AB =
a lorsque l'autre extrémité A est tirée le long
d'une droite. Une première généralisation vient
immédiatement à l'esprit : pourquoi ne pas tirer
l'extrémité A le long d'une courbe quelconque
G ? Dans ce cas, la courbe décrite
par B est appelée tractoire de
base G.
Désormais, je parlerai de
tractoires, en réservant le mot
tractrice à la première
tractoire, la tractoire historique, celle qui a pour base une droite
et qui a été construite dans la partie
2.1.
Tractoire à base
circulaire
|
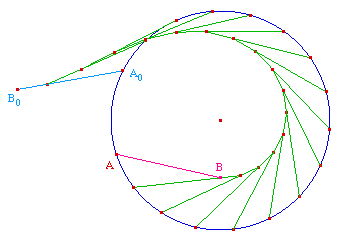
Prenons d'abord pour base la courbe la plus simple : le
cercle. Il est facile d'imaginer une construction analogue
à celle utilisée pour la tractrice dans la
partie 2.1. Soit
A0B0 la position initiale du fil
(A0 sur le cercle) et soit A un point quelconque
du cercle. On partage le segment [A0A] en
16 parties(en prenant soin que les points du partage restent
toujours sur le même arc) On applique 16 fois la macro
TractInst.mac de la
partie 2.1. Toutefois, pour
obtenir de belles courbes, il est conseillé de
créer aussi des macros correspondant à des
partages en 64 parties
TractC01.fig
ou la macro associée
TractC16.mac
d' objets initiaux A0,
B0 le cercle et le point A, et d'objet final le
point B.
|
A partir de cette construction, il est facile de
poursuivre pour réaliser une macro
TractC64.mac pour des partages
en 64 parties.
|
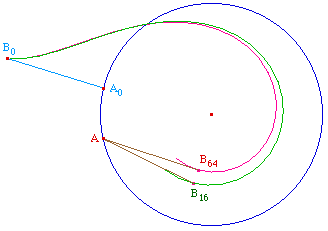
La tractoire du cercle est alors obtenue en demandant le
lieu de l'extrémité B lorsque l'autre
extrémité A décrit le cercle. Par sa
nature même, cette construction ne fonctionne que pour
un tour. Elle correspond à un fil que l'on tire dans
le sens des aiguilles d'une montre à partir de la
position initiale A0B0, et ce pendant
un tour, ci contre avec les deux macros partageant l'arc
(A0A) en 16 ou 64 parties.
TractC02.fig
|
.
|
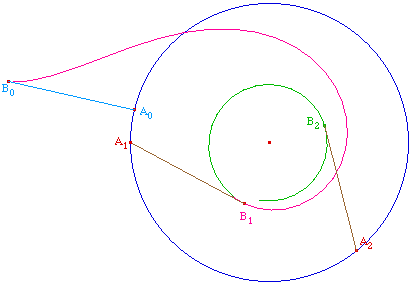
Si on veut simuler un second tour, il suffit,
après avoir effectué presque un tour, de
placer le point A proche de A0. Notons
A1B1 cette position du fil. On peut
alors recommencer la construction avec
A1B1 pour position initiale et avec un
nouveau point A2 sur le cercle. On obtient alors
le point B2 , dont le lieu est la " suite " de la
tractoire !
Ci contre on a fait la trace de B2 quand
A2 se déplace sur le cercle.
TractC03.fig
|
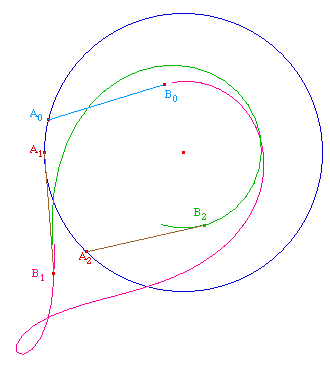
Avec B0 à
l'intérieur du cercle
Enfin, pour terminer en beauté ces considérations
générales, une tractoire à trois tours :
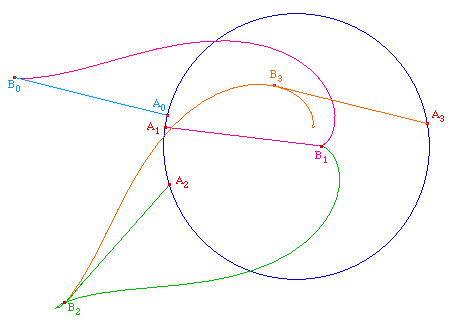
TractC04.fig
Le cas de la spirale tractrice
Dans le cas particulier où la longueur du fil est
égale au rayon du cercle de base, on retrouve une courbe
introduite par Varignon et appelée
spirale tractrice. Cette courbe jouit de
la propriété remarquable suivante :
" Les points de la spirale
tractrice où la tangente est parallèle à une
droite donnée passant par le centre du cercle de base sont
situés sur les deux cercles ayant même rayon que le
cercle de base et centrés aux points d'intersection de la
droite et du cercle de base ".
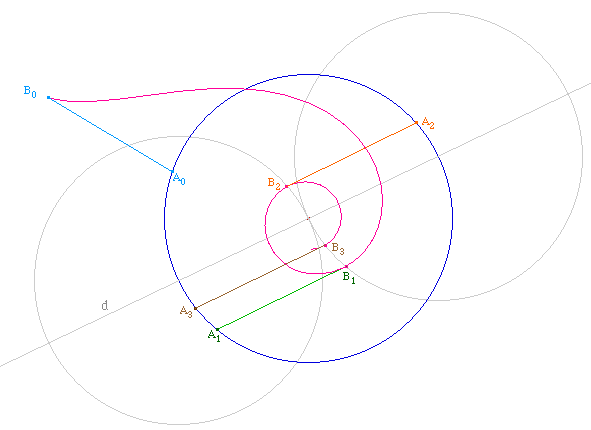
TractC05.fig
Grâce à son nouveau savoir-faire sur la construction
des tractoires, le lecteur curieux pourra expérimenter autour
de cette propriété et tenter de découvrir
comment elle se généralise à une tractoire
circulaire quelconque. Pour des démonstrations, voir F. Gomes
Teixeira, Traité des courbes spéciales remarquables
planes et gauches, rééd. Jacques Gabay, tome II, p.
91 et p. 96. Dans ce livre extraordinaire, on apprend aussi que
l'inverse de la spirale tractrice
par rapport à son cercle de base est une
développante de cercle.
Comment s'empêcher d'illustrer avec Cabri ce résultat
inoubliable ?
TractC06.fig
Extension aux coniques
|
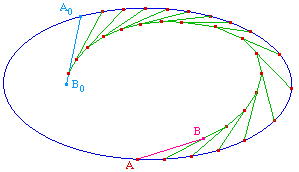
On peut facilement étendre la construction aux
coniques. En effet, dans Cabrti, le partage le segment
[A0A] en 16 parties par des
médiatrices successives respecte toujours le suivi
des intersections. On applique à nouveau 16 fois la
macro TractInst.mac de
la partie 2.1.
TractC07.fig
ou la macro associée
TraCnk16.mac
d' objets initiaux A0,
B0 la conique et le point A, et d'objet final le
point B.
|
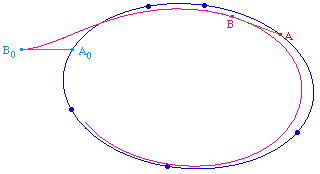
TractC08.fig
Cette extension aux coniques sera utile pour
l'intégration de certaines équations
différentielles; nous en reparlerons plus en détail
ultérieurement.
2.1 Construction de la tractrice |
2.2. Tractoire à base non rectiligne
2.3. Tractoire à directrice non
circulaire | 2.4. Construction des
logarithmes
[Introduction] [Histoire
de la tractrice] [Tractrice et autres tractoires]
[Application aux équations
différentielles]
[Tractrice et
pseudo-sphère] [Retour
"Courbes et équations"]
Menu général